Игорь Мерзляков - Квантовая химия в примерах

Если h=1, тогда D`=2.

Если h> 1 и h – чётное, то D`=12h 2—24h+14.

Если h> 1 и h – нечётное, тогда D`=12h 2—24h+12.

Заполним таблицу 2.1 полученными данными.

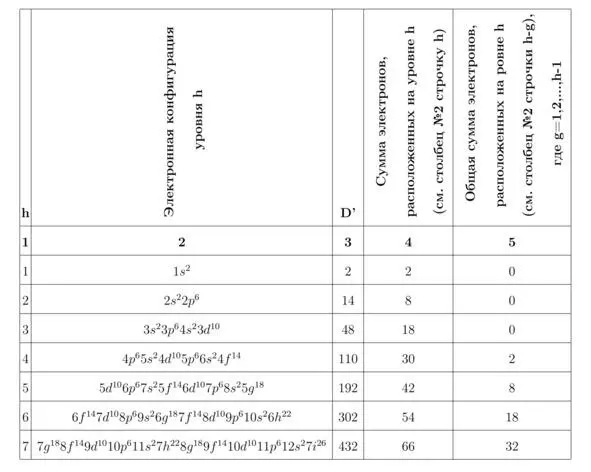
Таблица 2.1 Сводная таблица, подтверждающая справедливость периодического закона Менделеева, который можно применить к исследуемой модели атома.

Основными характеристиками, с помощью которых можно восстановить таблицу Д. И. Менделеева, являются соотношения между столбцами 3, 4 и 5 таблицы 2.1. Покажем, что данные соотношения сохраняются для каждого нового квантового уровня, задаваясь величинами из таблицы 2.1 в скобках (строка, столбец), тогда для чётных h> 3 получим:

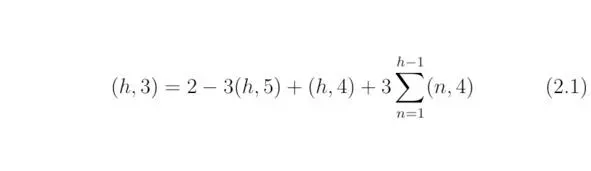
Для нечётных h> 4 и всех остальных h <4 справедливым будет следующее тождество:

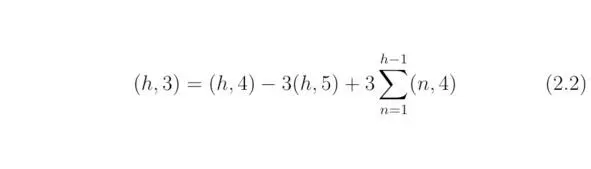
Итак, используя полученные в данном параграфе выражения, можно определить количество свободных потенциальных ям, которые располагаются на оболочках атомов, входящих в состав моделируемого химического соединения.

Рассматривая процессы, происходящие на уровне мельчайших взаимодействий, необходимо учитывать тот факт, что природа электрона носит корпускулярно-волновой характер. Если электрон проявляет волновую природу, тогда его физическая сущность будет соответствовать правилам математического описания волн. В том случае, когда электрон принимает корпускулярную форму, тогда появляется необходимость зафиксировать исследуемый фермион в той или иной точке пространства для измерения его координат или импульса. Если наблюдение за электроном не производится, тогда он может перемещаться относительно заданного базиса. Естественно, что говорить о движении электронов во время измерения (наблюдения за ними) в рамках данного подхода к задачам квантовой химии бессмысленно. Указанные свойства двойственной природы электронов необходимо взять на вооружение для последующего построения теории взаимодействия частиц, объединённых в химическую структуру.

Для получения химического соединения на практике необходимо, чтобы минимум 2 атома объединились в общую структуру. Таким образом, электроны, входящие в состав одного из атомов, будут совмещаться с потенциальными ямами, где нет электронов, другого химического элемента. Примером может послужить соединение, полученное из 2-х атомов, чей квантовый уровень равен h=2. В периодической таблице Менделеева наименования рассматриваемых атомов расположены во 2-м периоде, куда входят химические элементы, начиная от лития Li 3и заканчивая неоном Ne 10, где индексы 3 и 10 указывают на заряды соответствующих ядер. Потенциальные ямы обозначаются крестиками, если в них располагаются электроны (по одной частице на одну или несколько потенциальных ям). Пустые потенциальные ямы, где могут находиться электроны, но, вследствие недостаточной величины заряда атомного ядра, указанное расположение не последовало, обозначим треугольниками. Области синусоидальной функции, куда могут попасть положительно заряженные частицы, остаются незаполненными электронами (в них возможно зафиксировать позитроны). В центральную потенциальную яму атома (куба) помещается положительно заряженное ядро. Звездойобозначается потенциальная яма, полученная в результате совмещения крестика и треугольника. Подобное совмещение обеспечивает стабильность кристаллической структуры или молекулы при воздействии на квантовую систему извне. Большинство химических соединений, имеющих под собой теоретическое обоснование, возможно получить на практике при условии, что между атомами, входящими в состав той или иной кристаллической структуры или молекулы, будут присутствовать химические связи. На рисунке 3.1 продемонстрированы 2 соединённых между собой атома, расположенных отдельно друг от друга на изображении слева и совмещённых в общую структуру – справа.

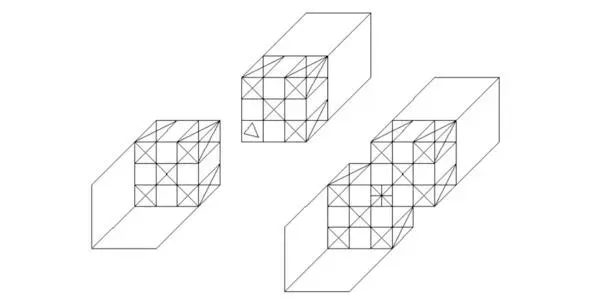
Рисунок 3.1 Соединение 2-х атомов в их вершинах.

Следующее возможное соединение, полученное из частиц, которые изображаются на рисунке 3.2, располагается вдоль их сторон. Треугольники, входящие в состав первого атома, находятся на одной прямой, вследствие чего в них легко попадают крестики (потенциальные ямы с электронами) другого химического элемента. В результате образуется гораздо более прочное соединение по сравнению с взаимодействием, показанным на рисунке 3.1.

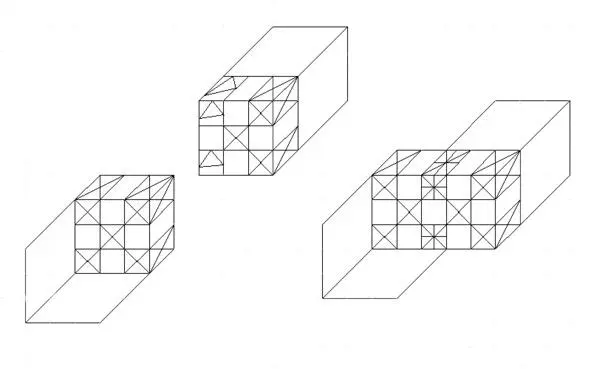
Рисунок 3.2 Соединение атомов вдоль одной плоскости (грани куба) в двух точках.

Наиболее сильное соединение возникает при совмещении атомов вдоль их граней. На рисунке 3.3 продемонстрирован пример такого соединения, где потенциальные ямы с крестиками объединяются с потенциальными ямами, помеченными треугольниками. Заметим, что на рисунке слева, расположенном на изображении 3.3, в центре граней атомов находятся треугольники. Соединение 2-х химических элементов возможно получить только в том случае, когда пустые потенциальные ямы будут заполняться электронами. Таким образом, в рассматриваемом примере следует говорить о существовании дырочной проводимости в веществе.

В процессе моделирования химических соединений необходимо учитывать незаполненные подуровни, потенциальные ямы которых не определяют химическую связь. В расчёте химического взаимодействия атомов будет участвовать некоторое количество потенциальных ям, а не электронов, поскольку отрицательно заряженные частицы с предыдущих уровней занимают в три раза больше потенциальных ям, чем электроны на заданном энергетическом уровне.

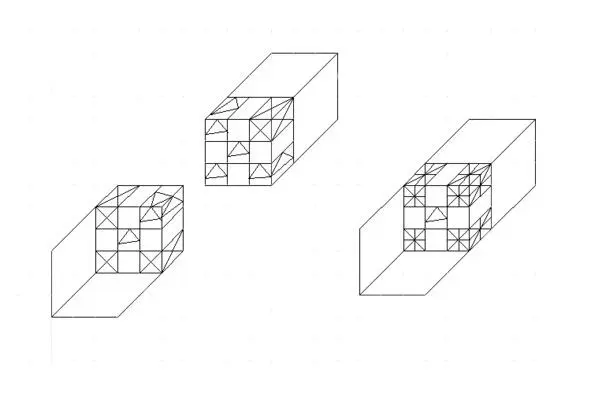
Рисунок 3.3 Соединение 2-х атомов вдоль одной плоскости (грани куба) в четырёх точках.

Ещё одним важным видом взаимодействия атомов, входящих в состав той или иной кристаллической решётки или молекулы, является такое расположение частиц, когда существует возможность составить стационарное решение уравнения Шрёдингера, полученное для химического соединения, которое не содержит в своей структуре звёздочек (см. рисунок 3.4). Для слоистых материалов, например графита, существует небольшое притяжение между двумерными кристаллическими структурами графена. В процессе моделирования не остаётся свободных треугольников в двумерной структуре графена, однако, исходя из особенностей решения уравнения Шрёдингера, полная энергия квантовой системы на практике примет минимальное значение, что обеспечит стабильность атомов, входящих в состав трёхмерного химического соединения. Расположение электронов в потенциальных ямах будет сохраняться до тех пор, пока не изменятся значения полупериодов пространства синусоидальной функции R x/m x, R y/m y, R z/m z. После преобразования сетки из потенциальных ям на частицы будут действовать только внешние силы. Таким образом, движение химических структур, не связанных общим решением уравнения Шрёдингера, можно описать, применяя законы классической механики.