Игорь Мерзляков - Квантовая химия в примерах

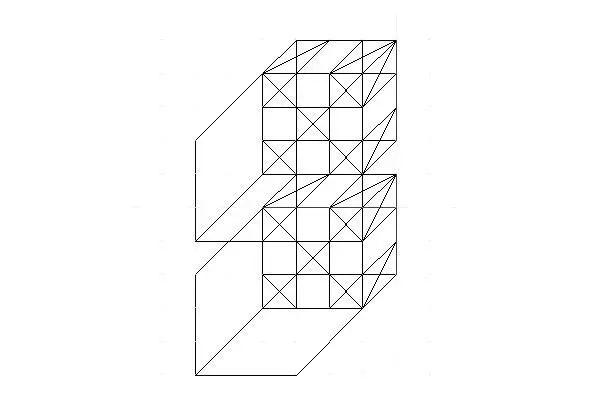
Рисунок 3.4 Ван-дер-Ваальсова связь.

Примечательно, что в слоистой структуре двумерные химические соединения, состоящие из атомов, будут смещены относительно друг друга.

Процесс формирования кристаллических структур и молекул, происходящий на практике, подразумевает в себе обмен электронами между атомами в химическом соединении. Если в структуре вещества остаются свободные потенциальные ямы с треугольниками, тогда выбранную модель чаще всего невозможно получить на практике, за исключением случаев наличия дырочной проводимости в кристалле или существования полностью свободных подуровней на рассматриваемом энергетическом уровне. Так, например, в структуре Na 2He для натрия Na орбиталь 3d 10останется незаполненной электронами. При моделировании молекулярных структур действуют аналогичные правила, позволяющие дать теоретическое обоснование химическим взаимодействиям, рассмотренным выше в этом разделе.

В начале XXI века на горизонте научных открытий появилось парадоксальное явление. Суть последнего заключается в том, что химические структуры, которые нельзя получить в нормальных условиях, могут существовать при высоких давлениях, исчисляемых в десятках и сотнях ГПа. Метод Оганова позволяет моделировать указанные структуры. Соединения, предсказанные алгоритмом А. Р. Оганова, бывают как слоистыми, так и носят пространственный характер, оставаясь цельными в трёхмерной системе координат. Вещества под давлением обладают как сверхпроводимостью, так и являются хорошими изоляторами электрического тока. В разделе 10 мы вернёмся к более подробному описанию свойств кристаллических решёток. Подход, изучаемый в этой книге, можно применить для предсказания строения химических структур, существующих как под высоким давлением, так и в нормальных условиях. В данной и последующих главах мы разберём ряд примеров химических соединений, модель которых возможно получить на практике.

А. Р. Оганов в программе «USPEX» разработал максимально результативный на сегодняшний день численный алгоритм, с помощью которого возможно составить ту или иную кристаллическую структуру с минимальным значением полной энергии. Время, которое необходимо затратить на моделирование кристаллов или молекул, в общем случае зависит не только от числа частиц, участвующих в расчёте, но и от количества полученных структур с минимальным значением полной энергии.

Принципы, позволяющие составить модель кристаллической структуры:

а) Потенциальные ямы, где могут располагаться отрицательно заряженные частицы, должны быть заполнены электронами. Однако данное условие окажется невыполнимым в том случае, когда на заданных энергетических уровнях, входящих в состав атомов вещества, будут существовать свободные подуровни или когда появится возможность получить на практике кристалл с дырочной проводимостью.

б) Между элементами кристаллической решётки должна существовать симметрия. Данное условие обеспечивает стабильность химической структуры.

в) Наряду с симметрией, в кристаллической решётке должна присутствовать периодичность. Под периодичностью понимают повторяемость элементов решётки в том или ином направлении. В случае, когда моделируется квазикристалл, то выполнение условия периодичности не требуется.

г) Моделируемые кристалл или молекула должны быть максимально компактными. Если заданная химическая структура занимает больший объём в пространстве, чем альтернативные соединения с похожим составом атомов, тогда исследуемое химическое соединение не будет существовать в природе, поскольку, согласно расчётным данным, полная энергия рассматриваемой квантовой системы примет отличное от минимального значение. Таким образом, атом водорода H, например, будет стремиться приблизиться к центру грани другого химического элемента, с которым происходит соединение.

Пример 4.1. Na 2He

Рассмотрим пример слоистой структуры, существующей под высоким давлением, в которой присутствуют атомы гелия He. В моделях кристаллических решёток видимые ядра обозначаются большим шрифтом, а невидимые – маленьким. В процессе расчёта химических взаимодействий необходимо определить количество треугольников и крестиков, участвующих в формировании кристаллической структуры из атомов, согласно соотношениям, которые были получены в разделе 2. Тогда количество треугольников, определяемое для гелия и натрия, составит:

He=0;

Na=48-30-11+10=17 плюс 2 свободно блуждающих электрона;

где 48 – количество потенциальных ям, расположенных на оболочке куба (атома) уровня h=3.

30 – количество электронов, находящихся на предыдущих оболочках куба (атома) уровней h=1 и h=2, в трёхкратном увеличении.

11 – порядковый номер, определяемый согласно таблице Менделеева для натрия Na.

10 – номер последнего химического элемента, расположенного на предыдущем уровне h=2.

Определим количество крестиков:

He=2; Na=48—17=31.

Изобразим схематично структуру Na 2He :

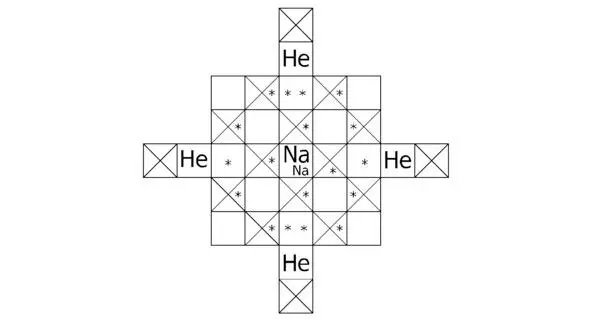
Рисунок 4.1 Вид «спереди» для структуры Na 2He.

Символом «*» обозначаются звёзды (потенциальные ямы, где треугольники совмещаются с крестиками).

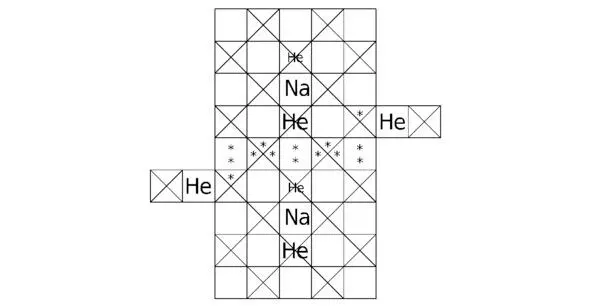
Рисунок 4.2 Вид «сверху» для структуры Na 2He.

Моделируя структуру Na 2He, необходимо учитывать тот факт, что 3d 10подуровень для натрия останется полностью свободным, следовательно количество треугольников в атомах Na составит 17—10+2=9, где 17 – полное число треугольников для натрия Na, а 10 – количество потенциальных ям, расположенных на незаполненном 3d 10подуровне. Аналогичным образом возможно вычесть 6 из 9: 9—6—2=1, поскольку заполнение электронами оболочек атомов натрия может остановиться на 3s 2 подуровне, где 6 – количество потенциальных ям, находящихся на свободной 3p 6 орбитали. Таким образом, на одном уровне при заполнении частицами подуровней s и p происходит конкуренция. С орбитали 4s 2 могут спускаться электроны на оболочку атома для заполнения свободных потенциальных ям (треугольников), однако, частицы также способны подниматься на более высокий уровень. По факту в структуре Na 2He электроны заполнят 4s 2подуровень, следовательно в выражении, полученном для вычисления количества треугольников, необходимо дополнительно учесть коэффициент, принимающий в расчёт две свободно блуждающие частицы.