Игорь Мерзляков - Путешествие в квантовую механику

© Игорь А. Мерзляков, 2022

ISBN 978-5-4498-1610-8

Создано в интеллектуальной издательской системе Ridero

Формирование положений по квантовой механике происходило на протяжении XX века. Многое удалось сделать, но осталось немало открытых вопросов, исследование которых постепенно перешло в новое тысячелетие. В этой книге мне хотелось бы поднять вопрос о фундаментальности квантовой физики. В процессе изучения материала данной работы мы рассмотрим исключительно нерелятивистские явления.

Принципы квантовой механики опираются на интуицию и согласованность теоретической базы знаний с экспериментальными данными.

В процессе научных изысканий, автор данного исследования получил новый подход к решению дифференциальных уравнений, который был положен в основу изучаемого в этой книге предмета.

Ещё одной причиной для написания этой работы послужила некоторая надежда на дальнейшее развитие квантовой физики. Однажды Р. Ф. Фейнман сказал: «Посмотрите на мир с другой стороны». Мне хотелось бы, чтобы указанная фраза стала девизом этой небольшой книги.

Контакты для связи:vk.com/garrydipray, iganmer@gmail.com, iganmer@yandex.ru.

В данной главе будут рассмотрены два метода, с помощью которых можно получить тот или иной физический закон, существующий в природе. Первый включает в себя исследование дифференциальных соотношений, дающих математическое обоснование физической реальности, а второй неразрывно связан с определением зависимостей в заданном наборе функций. Последние могут быть получены опытным путём или составлены в результате экстраполяции значений, входящих в состав решения того или иного дифференциального уравнения.

Справедливость методов, которые формулируются на основе анализа экспериментальных данных, изначально можно поставить под сомнение. Однако, применяя эмпирический подход на практике, возможно дать математическое обоснование тем выражениям, которые служат для описания физических явлений и процессов, происходящих в природе.

Начнём этот раздел с вывода уравнения Шрёдингера. Методика, позволяющая получить зависимости, существующие между физическими величинами, которые входят в состав указанного уравнения, носит интуитивный характер. Однако, как будет показано ниже, решение уравнения Шрёдингера даёт верное описание физической реальности в условиях мельчайших взаимодействий.

В 1924 году французский физик Луи де Бройль выдвинул смелую гипотезу, согласно которой корпускулярно-волновой дуализм имеет универсальный характер (электрон может быть описан математически как в виде волны, так и в виде частицы) Исходя из гипотезы де Бройля, каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы, остаются такими же, как и в случае электромагнитного излучения веществом. Полную энергию E и импульс частицы p возможно выразить через круговую частоту ν, длину волны λ и приведённую постоянную Планка ħ, тогда:

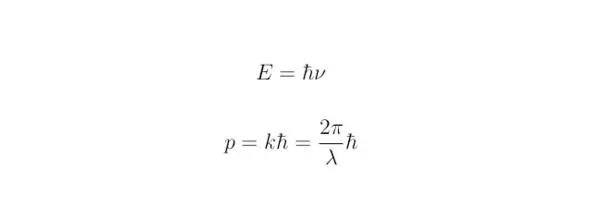
где величина k=2π/λ;

Для того, чтобы получить уравнение Шрёдингера, необходимо записать закон сохранения энергии волны де Бройля. Величина E представляет собой сумму кинетической E kи потенциальной U (x,y,z) энергии:

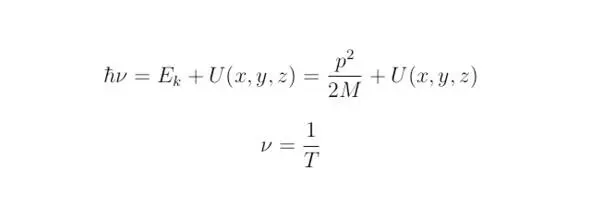
где M – масса частицы. T – период волны Де Бройля.

Длину волны Де Бройля можно выразить через скорость V, тогда:

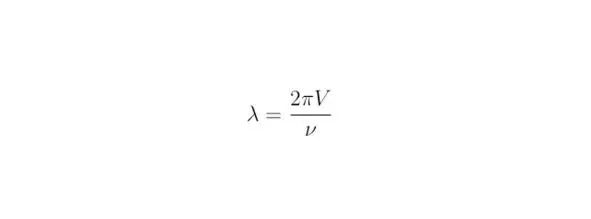
Вывод уравнения Шрёдингера следует производить в трёхмерном пространстве С 3, в котором происходит изменение физических величин во времени. Однако для упрощения вычислений будем использовать одномерную систему координат. Закон сохранения энергии волны Де Бройля можно выразить в виде тождества:

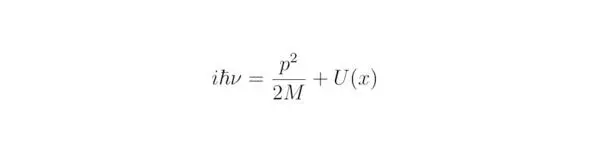
Выполним следующие преобразования:

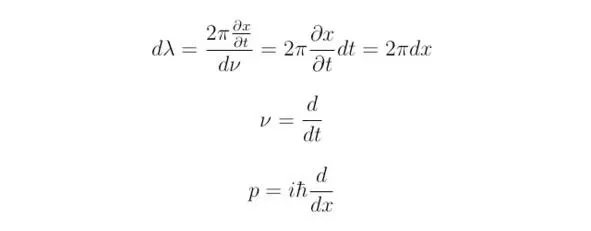
где t – время, а x – координата.

Следствие, которое можно почерпнуть из данных преобразований, гласит, что для справедливости выкладок, полученных в результате вывода уравнения Шрёдингера, необходимо ввести новую функцию под знаки производных. В процессе преобразований был найден оператор, который представляет из себя закон сохранения энергии, записанный для исследуемой волны Де Бройля. Искомую величину принято обозначать как волновую функцию ψ, тогда:

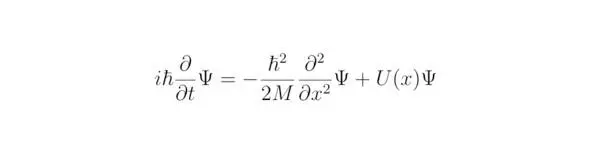
Последнее выражение носит своё название в честь учёного, который обобщил в своих научных исследованиях физические законы, описывающие волновую природу реальности. Главным достижением Эрвина Шрёдингера стало уравнение, сыгравшее огромную роль в развитии теоретических и практических результатов в квантовой физике. Общий вид уравнения Шрёдингера мы получили в этом параграфе.

Обычно с изучением школьной программы принято брать на веру справедливость основных положений, позволяющих осуществить вывод фундаментальных законов физики. В этом разделе мы разберём принципы получения таких зависимостей, которые существуют между физическими величинами, входящими в состав указанных законов.

Для того, чтобы выполнить дальнейшие математические преобразования, необходимо определить понятие «зависимости физических величин», значения которых могут быть выражены через изменение прочих независимых переменных.

Исходя из формулировки о зависимости величины F от функций f j(x j), полученных для переменных x j, заданные выражения f j(x j) следует перемножать между собой только в том случае, когда они окажутся независимыми. Иначе говоря, изменение функции f j(x j) будет происходить без взаимного влияния её значений на другие выражения f o(x o), o≠j. Потребуем, чтобы количество независимых переменных соответствовало величине N. Итак, функцию F можно выразить в виде соотношения, куда входят значения γ j. Каждое из значений γ jсоответствует коэффициенту пропорциональности (+1 или -1), который представляет из себя степень функции f j(x j) γj, следовательно: