Игорь Мерзляков - Путешествие в квантовую механику

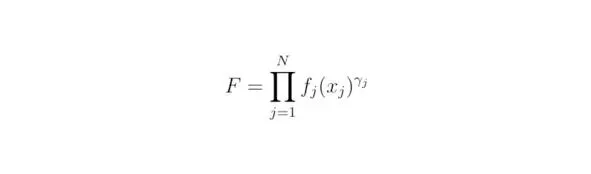
Наглядным примером применения эмпирического подхода к решению физических задач может послужить закон Кулона, полученный для силы электростатического взаимодействия. Таким образом, следующие выражения могут быть определены как независимые между собой функции:

f 1(x 1) – произведение зарядов q 1q 2.

f 2 – коэффициент пропорциональности k.

f 3(x 3) – квадрат расстояния между частицами f 3(x 3) =|r 1-r 2| 2. r p – радиус-вектор, построенный из начала координат в точку с зарядом q p. p=1,2.

Хорошо известно, что сила Кулона прямо пропорциональна f 1(x 1) и f 2(γ j=1), но обратно пропорциональна f 3(x 3) (γ 3=-1).

Запишем закон Кулона, вид которого можно получить из анализа экспериментальных данных:

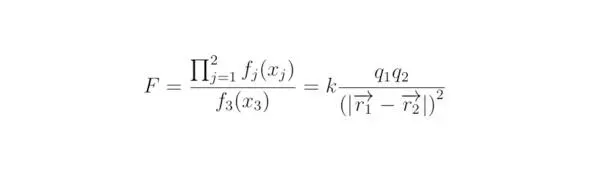
Если величины f j(x j) и g j(x j) окажутся взаимно зависимыми, тогда справедливым будет тождество:

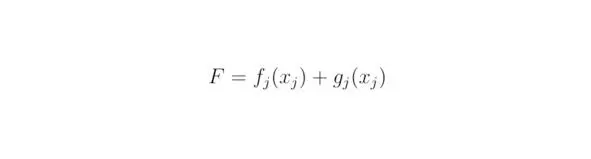
Функции f j(x j) и g j(x j) могут носить более сложный математический характер, нежели степенные выражения. Довольно часто эмпирическим методом невозможно получить тот или иной закон природы, тогда исследователи прибегают к составлению дифференциальных уравнений, например, дифференциальных уравнений в частных производных. Решение последних иногда затрудняется, вследствие невысокой производительности современных компьютеров, в подобных случаях используют суперкомпьютеры.

Пришло время ознакомиться с третьим разделом этой книги, где мы сформулируем общее представление о трудностях, возникающих в процессе решения уравнения Шрёдингера. В следующей главе будет рассмотрен метод, позволяющий отыскать решение произвольно заданного дифференциального уравнения в частных производных.

Применяя методику, которая будет изложена в этом параграфе, можно найти решение того или иного дифференциального уравнения и выявить характерные черты эволюции искомой функции во времени.

Рассмотрим ряд Фурье в одномерной системе координат. Преобразуем его к виду, в который входит набор линейных функций F k, отображаемых на отрезках (kΔx, (k+1) Δx) вдоль оси x ∈ (0,R x), где Δx – размер интервалов, куда заключены значения функций F k, k – номер вычислительной операции, k∈ N.Следовательно:

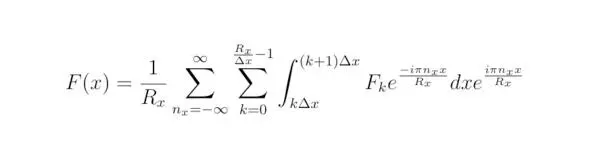
Тригонометрический ряд, который можно получить для произвольной кусочно-дифференцируемой функции F (x,y,z), задаваемой на отрезках (k Δx, (k+1) Δx) для x ∈ (0,R x), (j Δy, (j+1) Δy) для y∈ (0,R y) и (p Δz, (p+1) Δz) для z∈ (0,R z), преобразуется к виду:

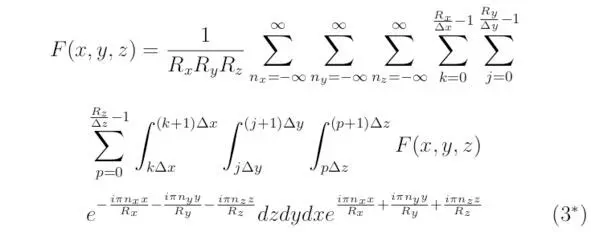
Таким образом, из выбранных линейных комбинаций F k, определяемых на отрезках (kΔx, (k+1) Δx), возможно построить кусочно-дифференцируемую функцию F (x), тогда:

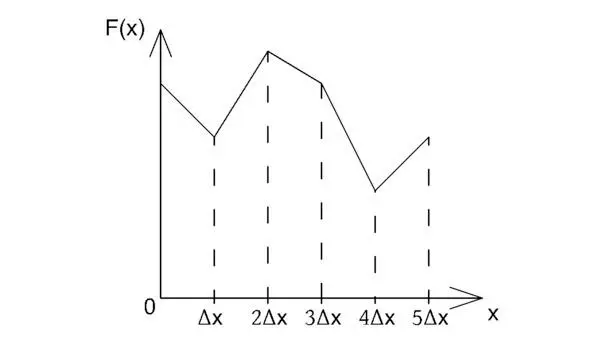
Рисунок 3.1 Интерполяция одномерной функции F (x).

Пусть Q∈ Cявляется решением произвольно заданного дифференциального уравнения в частных производных. Введём обозначения для функций a, b, значения которых будут соответствовать вещественной и мнимой части тождества Q=a+ib. Для того, чтобы отыскать решение произвольно заданного дифференциального уравнения, необходимо с помощью метода Эйлера определить закон изменения функции Q во времени. Следует отметить, что рассматриваемый способ решения дифференциальных уравнений является не единственным, однако, в рамках данной книги остановимся на нём, как на простом и наиболее наглядном. Произвольно заданное параболическое дифференциальное уравнение с частными производными возможно преобразовать к общему виду, следовательно:

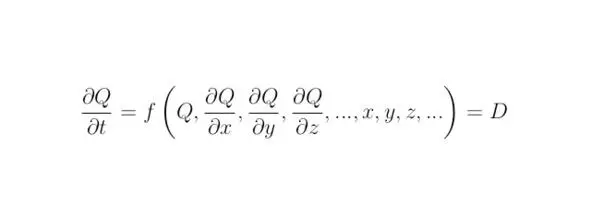
Разложим в ряд Фурье решение Q, тогда:

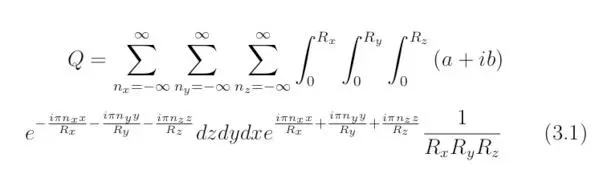
Определим частные производные порядка s по координате x p, входящие в состав выражения D, следовательно:

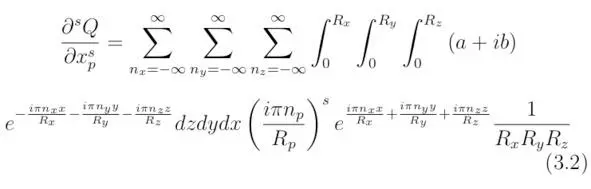
здесь n pи R p – коэффициенты при координате x p.

В случае расходимости ряда (3.2) применяется следующее преобразование:

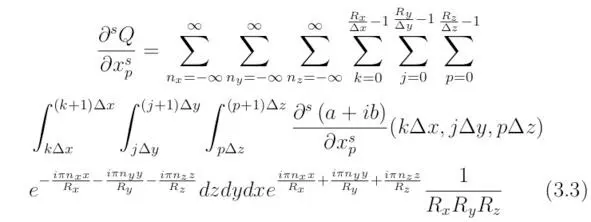
Вид функции ∂ sQ/∂x, который можно получить для точек, находящихся в пространстве C 3, формируется согласно уравнению (3.3). Выполним интерполяцию значений выражения D. Если рассматривается одномерный случай, то каждой точке, расположенной на оси D, необходимо поставить в соответствие отрезок (oΔx g, (o+1) Δx g), находящийся на оси x g. Следовательно, в трёхмерном пространстве справедливым будет соотношение:

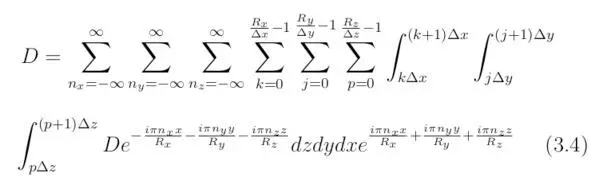
Определим частную производную решения Q по времени, тогда:

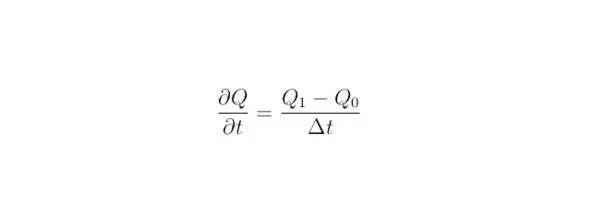
Выполним следующие преобразования:

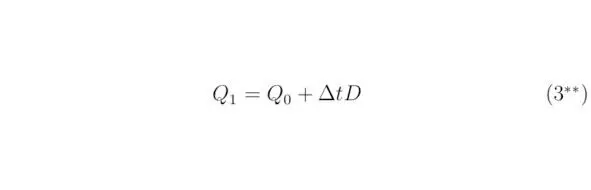
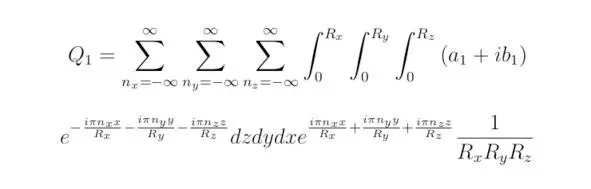
Выражения Q 0и Q будут тожественно равны друг другу в рамках одной итерации. Подставим величины Q 1, D и Q в уравнение (3 **), а затем произведём обратное преобразование Фурье. В результате получим соотношение:

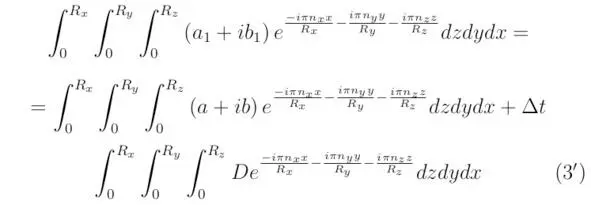
Определим действительную часть решения Q 1, тогда:

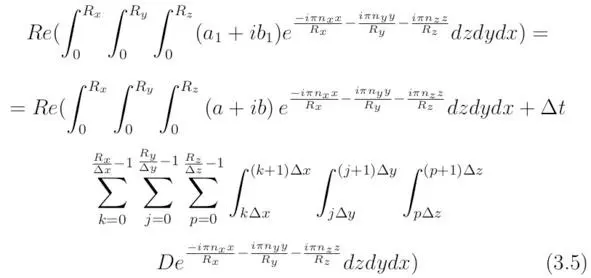
Вместе с тем справедливым будет тождество, полученное для мнимой части уравнения (3`):