Игорь Мерзляков - Путешествие в квантовую механику

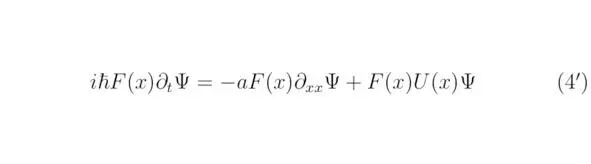
Заменим неизвестные переменные в тождестве (4`) на соотношения A, B, C, тогда:

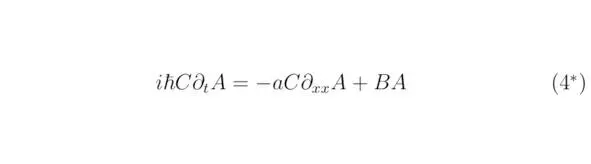
Выражение (4 *) содержит в себе общий член exp (iπm xx/R) exp (iπn xx/R). Необходимо сократить последний, оставив в результате только коэффициенты тригонометрического ряда:

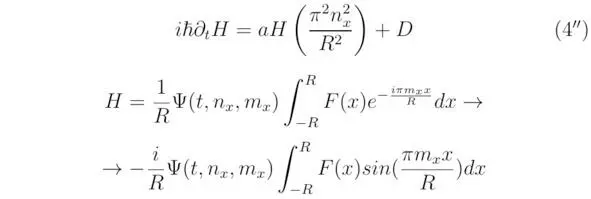
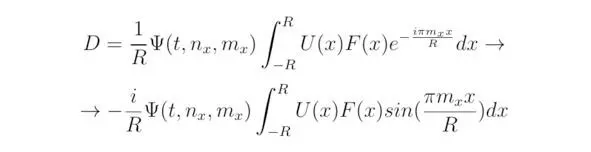
Разделим переменные относительно ψ (t, n x, m x), тогда:

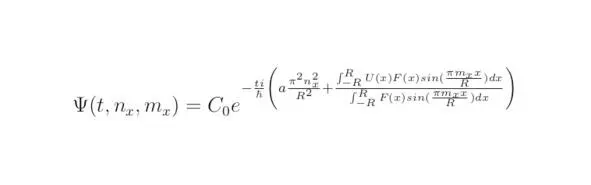
Коэффициент C 0возможно определить исходя из соотношения, полученного для нормированной вероятности (см. раздел 3.3). В рассматриваемом примере существует зависимость величины C 0от времени t. Таким образом, следует потребовать постоянство коэффициента C 0в случае решения стационарного уравнения Шрёдингера.

Область определения волновой функции будет лежать в пределах отрезка (-R,R). В некоторых теоретических случаях допустимо принимать R=∞, тогда:

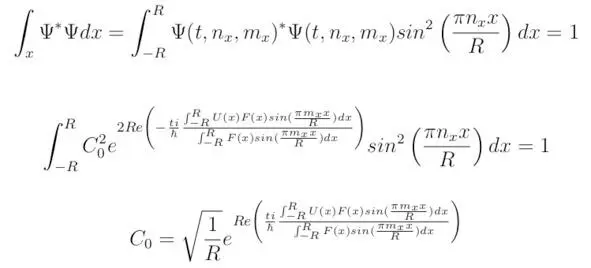
Энергию электрона E можно определить из стационарного одномерного уравнения Шрёдингера, следовательно:

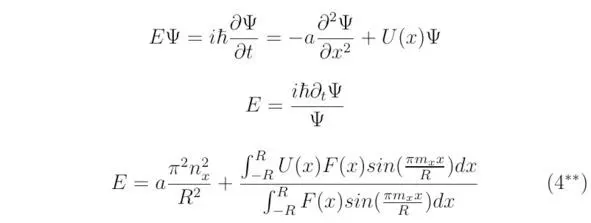
Для трёхмерного базиса величина полной энергии составит:

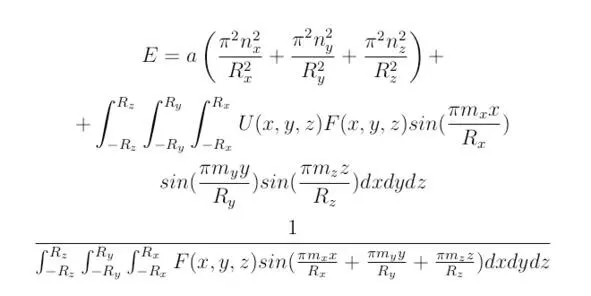
В заключение следует отметить, что величина E часто не обладает конкретно заданным значением, поскольку в выражении, полученном для полной энергии E, присутствуют произвольные функции: F (x) для одномерной или F (x,y,z) для трёхмерной системы координат. Исходя из неопределённости величины E, находящейся в зависимости от значений непостоянной потенциальной энергии U (x,y,z) ≠const, вид функций F (x) и F (x,y,z) установить невозможно.

Доказательство единственности аналитического решения уравнения Шрёдингера в рамках данного подхода не имеет смысла, за исключением случая U (x) =const, который был подробно рассмотрен в главе 3.

Таким образом, опираясь на предложенную в данном параграфе методику, следует констатировать тот факт, что величина полной энергии E, выраженная в общем виде, будет зависеть от случайных процессов, протекающих в квантовой системе.

Значения функции F (x) должны быть фиксированными во времени в случае решения стационарного уравнения Шрёдингера. Вместе с тем в нестационарных условиях данное требование не является обязательным.

Если функции ψ 1и ψ 2являются волновыми, то их линейная суперпозиция ψ 3= c 1ψ 1+ c 2ψ 2описывает некоторое состояние квантовой системы. В том случае, когда измерение определённой физической величины f в состоянии ψ 1приводит к результату f 1, а в состоянии ψ 2 – к результату f 2, тогда измерение состояния ψ 3приведёт к результатам f 1или f 2с вероятностями |c 1| 2 и |c 2| 2 соответственно.

Поскольку уравнение Шрёдингера является линейным, то произвольно заданная комбинация его решений выражается в виде суммы собственных состояний волновой функции.

Концепция мысленного эксперимента кота Шрёдингера заключается в следующей идее. В ящик помещаются банка с ядом, молоточный механизм с детектором, который фиксирует ядерный распад, и кот, изначально живой. В случае распада ядра срабатывает детектор, который приводит в движение молоточный механизм, разбивающий сосуд с ядом, вследствие чего кот умирает. Согласно квантовой механике, если над ядром не производится наблюдение, то его состояние описывается суперпозицией двух состояний – распавшегося и нераспавшегося, следовательно кот, сидящий в ящике, и жив, и мёртв одновременно. Если же ящик открыть, то экспериментатор может увидеть только какое-нибудь одно конкретное состояние – «ядро распалось, кот мёртв» или «ядро не распалось, кот жив».

В квантовой механике коллапс волновой функции происходит в том случае, когда волновая функция (первоначально в суперпозиции нескольких собственных состояний) сводится к одному собственному состоянию, вследствие взаимодействия квантовой системы с внешним миром. Это взаимодействие в дальнейшем будем называть «наблюдением». Под нормированной суперпозицией понимается сумма нормированных волновых функций. Последние являются взаимно зависимыми. Примечательно, что объединенная волновая функция продолжает подчиняться уравнению Шрёдингера.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.