Николай Глинка - Общая химия
- Название:Общая химия
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Николай Глинка - Общая химия краткое содержание
Учебное пособие предназначено для студентов нехимических специальностей высших учебных заведений. Оно может служить пособием для лиц, самостоятельно изучающих основы химии, и для учащихся химических техникумов и старших классов средней школы.
Легендарный учебник, переведенный на многие языки стран Европы, Азии, Африки и выпущенный общим тиражом свыше 5 миллионов экземпляров.
При изготовлении файла, использован сайт http://alnam.ru/book_chem.php
Общая химия - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Разумеется, найденное выражение для энергии электрона относится к упрощенной модели атома. Но и для реального атома решение уравнения Шредингера также приводит к выводу о квантованности энергетических состояний электрона в атоме.
Модель одномерного атома позволяет понять, почему электрон, находящийся в атоме в стационарном состоянии, не излучает электромагнитной энергии (второй постулат теории Бора). Согласно модели Бора- Резерфорда, электрон в атоме совершал непрерывное движение с ускорением, т.е. все время менял свое состояние; в соответствии с требованиями электродинамики, он должен при этом излучать энергию. В одномерной модели атома стационарное состояние характеризуется образованием стоячей волны де Бройля; пока длина этой волны сохраняется постоянной, остается неизменным и состояние электрона, так что никакого излучения происходить не должно.
Становится ясным и вопрос о состоянии электрона при переходе из одного стационарного состояния в другое (в терминологии Бора — с одной стационарной орбиты на другую). Если, например, электрон из состояния, отвечающего рис. 6, а, переходит в состояние, соответствующее рис. 6, б, то во время этого перехода длина волны де Бройля будет иметь переменное значение, не отвечающее условию образования стоячей волны. Именно поэтому состояние электрона в этот промежуток времени будет неустойчивым; оно будет меняться до тех пор, пока длина волны де Бройля не будет вновь соответствовать условию образования стоячей волны, т.е. пока электрон не окажется в новом стационарном состоянии.
- 73 -
В упрощенной одномерной модели атома положение электрона относительно ядра определяется одной координатой, а его состояние — значением одного квантового числа. В двумерной (плоской) модели атома положение электрона определяется двумя координатами; в соответствии с этим, его состояние характеризуется значениями двух квантовых чисел. Аналогично в трехмерной (объемной) модели атома состояние электрона определяется значениями трех квантовых чисел. Наконец, изучение свойств электронов, входящих в состав реальных атомов, показало, что электрон обладает еще одной квантованной физической характеристикой (так называемый спин, см. § 30), не связанной с пространственным положением электрона. Таким образом, для полного описания состояния электрона в реальном атоме необходимо указать значения четырех квантовых чисел.
28. Главное квантовое число.
Итак, в одномерной модели атома энергия электрона может принимать только определенные значения, иначе говоря — она квантована . Энергия электрона в реальном атоме также величина квантованная. Возможные энергетические состояния электрона в атоме определяются величиной главного квантового числаn, которое может принимать положительные целочисленные значения: 1, 2, 3 ... и т.д. Наименьшей энергией электрон обладает при n = 1; с увеличением n энергия электрона возрастает. Поэтому состояние электрона, характеризующееся определенным значением главного квантового числа, принято называть энергетическим уровнемэлектрона в атоме: при n = 1 электрон находится на первом энергетическом уровне, при n = 2 — на втором и т.д.
Главное квантовое число определяет и размеры электронного облака . Для того чтобы увеличить размеры электронного облака, нужно часть его удалить на большее расстояние от ядра. Этому препятствуют силы электростатического притяжения электрона к ядру, преодоление которых требует затраты энергии. Поэтому бОльшим размерам электронного облака соответствует более высокая энергия электрона в атоме и, следовательно, большее значение главного квантового числа n. Электроны же, характеризующиеся одним и тем же значением главного квантового числа, образуют в атоме электронные облака приблизительно одинаковых размеров; поэтому можно говорить о существовании в атоме электронных слоевили электронных оболочек, отвечающих определенным значениям главного квантового числа.
Для энергетических уровней электрона в атоме (т.е. для электронных слоев, или оболочек), соответствующих различным значениям n, приняты следующие буквенные обозначения:
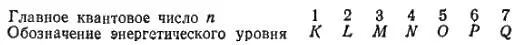
29. Орбитальное квантовое число. Формы электронных облаков.
Не только энергия электрона в атоме (и связанный с ней размер электронного облака) может принимать лишь определенные значения. Произвольной не может быть и форма электронного облака. Она определяется орбитальным квантовым числом l(его называют также побочным, или азимутальным), которое может принимать целочисленные значения от 0 до ( n — 1), где n — главное квантовое число. Различным значениям n отвечает разное число возможных значений l. Так, при n=1 возможно только одно значение орбитального квантового числа — нуль (l=0), при n=2 может быть равным 0 или 1, при n=3 возможны значения l, равные 0, 1 и 2, вообще, данному значению главного квантового числа n соответствуют n различных возможных значений орбитального квантового числа.
Вывод о том, что формы атомных электронных облаков не могут быть произвольными, вытекает из физического смысла квантового числа l. Именно, оно определяет значение орбитального момента количества движения электрона; эта величина, как и энергия, является квантованной физической характеристикой состояния электрона в атоме.
Напомним, что орбитальным моментом количества движения 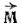 частицы движущейся вокруг центра вращения по некоторой орбите, называется произведение
частицы движущейся вокруг центра вращения по некоторой орбите, называется произведение 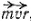 , где m — масса частицы,
, где m — масса частицы, 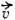 - ее скорость,
- ее скорость, 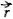 - радиус-вектор, соединяющий центр вращения с частицей (рис. 7). Важно отметить, что
- радиус-вектор, соединяющий центр вращения с частицей (рис. 7). Важно отметить, что 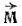 - векторная величина; направление этого вектора перпендикулярно плоскости, в которой расположены векторы
- векторная величина; направление этого вектора перпендикулярно плоскости, в которой расположены векторы  и
и 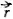 .
.
Определенной форме электронного облака соответствует вполне определенное значение орбитального момента количества движения электрона 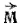 . Но поскольку
. Но поскольку 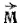 может принимать только дискретные значения, задаваемые орбитальным квантовым числом l, то формы электронных облаков не могут быть произвольными: каждому возможному значению l соответствует вполне определенная форма электронного облака.
может принимать только дискретные значения, задаваемые орбитальным квантовым числом l, то формы электронных облаков не могут быть произвольными: каждому возможному значению l соответствует вполне определенная форма электронного облака.
Интервал:
Закладка:








