Николай Глинка - Общая химия

- 80 -

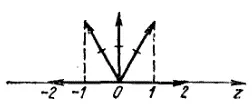
Рис. 19. К возможному набору значений магнитного квантового числа.

Стрелками показаны допустимые направления орбитального момента количества движения.

Набор возможных значений m можно пояснить следующим образом. Выберем некоторое направление в пространстве, например, ось z (рис. 19). Каждому направлению вектора заданной длины (в рассматриваемом случае — орбитального квантового числа l*) соответствует определенное значение его проекции на ось z. Из уравнения Шредингера следует, что эти направления могут быть только такими, при которых проекция вектора l на ось z равна целому числу (положительному или отрицательному) или нулю; значение этой проекции и есть магнитное квантовое число m. На рис. 19 представлен случай, когда l=2. Здесь m=2, если направления оси z и вектора l совпадают; m=-2, когда эти направления противоположны; m=0, когда вектор l перпендикулярен оси z; возможны и такие направления вектора l, когда m принимает значения ±1. Таким образом, магнитное квантовое число может принимать 2l+1 значений.

Квантовое число m получило название магнитного, поскольку от его значения зависит взаимодействие магнитного поля, создаваемого электроном, с внешним магнитным полем. В отсутствие внешнего магнитного поля энергия электрона в атоме не зависит от значения m. В этом случае электроны с одинаковыми значениями n и l, но с разными значениями m обладают одинаковой энергией.

Однако при действии на электрон внешнего магнитного поля энергия электрона в атоме изменяется, так что состояния электрона, различающиеся значением m, различаются и по энергии. Это происходит потому, что энергия взаимодействия магнитного поля электрона с внешним магнитным полем зависит от величины магнитного квантового числа. Именно поэтому в магнитном поле происходит расщепление некоторых атомных спектральных линий; вместо одной линии в спектре атома появляются несколько (так называемый эффект Зеемана).

Состояние электрона в атоме, характеризующееся определенными значениями квантовых чисел n, l и m, т.е. определенными размерами, формой и ориентацией в пространстве электронного облака, получило название атомной электронной орбитали.

На рис. 20 приведены формы и расположение в пространстве электронных облаков, соответствующих 1s-, 2p- и 3d-орбиталям. Поскольку s-состоянию (l=0) соответствует единственной значение магнитного квантового числа (m=0), то любые возможные расположения s-электронного облака в пространстве идентичны. Электронные облака, отвечающие p-орбиталям (l=0), могут характеризоваться тремя различными значениями m; в соответствии с этим они могут располагаться в пространстве тремя способами (рис. 20).

* Более строго следует рассматривать проекцию на ось z не орбитального квантового числа l, а определяемого им орбитального момента количества движения М.

- 81 -

При этом три p-электронных облака ориентированы во взаимно перпендикулярных направлениях, которые обычно принимают за направления координатных осей (x, y или z); соответствующие состояния электронов принято обозначать p x, p yи p z. Для d-орбиталей (l=2) возможно уже пять значений магнитного квантового числа и соответственно пять различных ориентаций d-электронных облаков в пространстве.

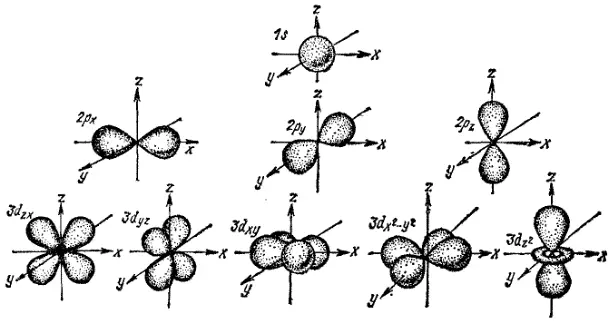
Рис. 20. Формы и пространственная ориентация электронных облаков 1s-, 2p- 3d-электронов.

Исследования атомных спектров привели к выводу, что, помимо квантовых чисел n, l и m, электрон характеризуется еще одной квантовой величиной, не связанной с движением электрона вокруг ядра, а определяющей его собственное состояние. Эта величина получила название спинового квантового числаили просто спина(от английского spin — кручение, вращение); спин обычно обозначают буквой s. Спин электрона может иметь только два значения: +1/2 или -1/2; таким образом, как и в случае остальных квантовых чисел, возможные значения спинового квантового числа различаются на единицу.

Кроме орбитального момента количества движения, определяемого значением l, электрон обладает и собственным моментом количества движения, что можно упрощенно рассматривать как результат вращения электрона вокруг своей оси. Проекция собственного момента количества движения электрона на избранное направление (например, на ось z) и называется спином.

Четыре квантовых числа — n, l, m и s — полностью определяют состояние электрона в атоме.

В атоме водорода электрон находится в силовом поле, которое создается только ядром. В много электронных атомах на каждый электрон действует не только ядро, но и все остальные электроны. При этом электронные облака отдельных электронов как бы сливаются в одно общее многоэлектронное облако.

- 82 -

Точное решение уравнения Шредингера для таких сложных систем связано с большими затруднениями и, как правило, недостижимо. Поэтому состояние электронов в сложных атомах и в молекулах определяют путем приближенного решения уравнения Шредингера.

Общим для всех приближенных методов решения этого уравнения является так называемое одноэлектронное приближение, т.е. предположение, что волновая функция много электронной системы может быть представлена в виде суммы волновых функций отдельных электронов. Тогда уравнение Шредингера может решаться отдельно для каждого находящегося в атоме электрона, состояние которого, как и в атоме водорода, будет определятся значениями квантовых чисел n, l, m и s. Однако и при этом упрощении решение уравнения Шредингера для много электронных атомов и молекул представляет весьма сложную задачу и требует большого объема трудоемких вычислений. В последние годы подобные вычисления выполняются, как правило, с помощью быстродействующих электронных вычислительных машин, что позволило произвести необходимые расчеты для атомов всех элементов и для многих молекул.

Исследование спектров многоэлектронных атомов показало, что здесь энергетическое состояние электронов зависит не только от главного квантового числа n, но и от орбитального квантового числа l. Это связано с тем, что электрон в атоме не только притягивается ядром, но и испытывает отталкивание со стороны электронов, расположенных между данным электроном и ядром. Внутренние электронные слои как бы образуют своеобразный экран, ослабляющий притяжение электрона к ядру, или, как принято говорить, экранируютвнешний электрон от ядреного заряда. При этом для электронов, различающихся значением орбитального квантового числа l, экранирование оказывается неодинаковым.