Джон Дрейер - История астрономии. Великие открытия с древности до Средневековья

Вернемся же теперь к не вызывающим сомнения результатам серьезного труда по этому вопросу, который затрагивает только Солнце и Луну. От Аристотеля («Метеорологика», I, 8, с. 345 b) мы узнаем, что уже в его дни проблема размера и удаленности Солнца и Луны уже начала привлекать внимание. «Суда» (в главе «Философы») приписывает его современнику Филиппу Опунтскому авторство книг о расстоянии до Солнца и Луны, о размерах Солнца, Луны и Земли, о лунных затмениях и планетах. Евдокс, как мы уже видели, считал, что диаметр Солнца в 9 раз больше диаметра Луны и, следовательно, расстояние до Солнца в 9 раз больше расстояния до Луны, так как видимый размер обоих светил кажется одинаковым. Архимед, упоминая это, прибавляет, что его отец [164]Фидий вычислил это отношение как 12:1. Сам Архимед исходил из отношения 30:1. Откуда взялись эти цифры, нам уже никак не узнать, однако есть вероятность, что методы, которыми пользовался Аристарх в следующем веке, на самом деле выработаны Евдоксом. Мы уже говорили, что Аристарх попытался определить относительные расстояния до Солнца и Луны и нашел, что первое примерно в 18—20 раз больше второго. В книге «О размерах и расстояниях Солнца и Луны» он также указывает, каким методом определил расстояние до Солнца, который, по Птолемею, применял и Гиппарх и которым астрономы пользовались еще шестнадцать веков. Он основан на наблюдениях за шириной земной тени на среднем расстоянии, на котором Луна пересекает ее во время лунных затмений. На рисунке ρ составляет половину этой угловой ширины, найденной измерением времени, которое требуется Луне, чтобы пересечь тень, тогда как г — угловой радиус Солнца, а ☉ и ☾ – параллаксы Солнца и Луны. Очевидно, что

По Гиппарху, г = 16′36″55′″ и ρ в 2½, раза больше («Синтаксис», IV, 8), и, если мы вместе с Аристархом примем ☾ = 19 ☉, это дает ☉ = 2′54″.

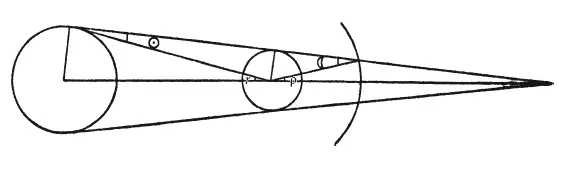
Но Гиппарх не удовольствовался этим методом нахождения суммы параллаксов Солнца и Луны, который может служить лишь для нахождения лунного параллакса; напротив, он, видимо, знал, что солнечный параллакс он таким методом выяснить не сможет в силу ошибок наблюдения, которых невозможно избежать. Из слов Птолемея (V, 11) представляется, что Гиппарх попытался найти пределы, в которых может лежать солнечный параллакс, чтобы согласовать наблюдения и расчеты в случае солнечного затмения, когда может проявиться разница параллаксов Солнца и Луны, тогда как сумму параллаксов можно было найти с помощью лунных затмений. Естественно, этот метод не дал никаких результатов, так что Гиппарх не был даже уверен, можно ли вообще определить солнечный параллакс или можно ли принять его равным 0. Во втором случае вышеприведенные значения для г и ρ дают ☾ = 58′9″14′″, что соответствует расстоянию до Луны, равному 59,1 полудиаметра Земли, и в 3½ раза больше полудиаметра Луны. Птолемей не говорит, какой верхний предел нашел Гиппарх, но, вероятно, Клеомед имел его в виду, сказав (II, 1), что Гиппарх доказал, что Солнце в 1050 раз больше Земли. Поскольку здесь речь идет об объеме, полудиаметр Солнца оказывается в 10/ 6раза больше полудиаметра Земли, а полудиаметр Луны – в 1 : 3 2/ 5раза (эти данные принимал Птолемей), и расстояния до Луны и Солнца соответственно равны 60 5/ 6и 2103 земным радиусам. Теон приводит среднее между этими предельными значениями, утверждая, что Гиппарх полагал, что Солнце в 1880 раз больше Земли, то есть его радиус в 12⅓ раза больше, расстояние равно 2550 земным радиусам, радиус Луны равен 12/ 41= 0,29, а ее расстояние – 60,5 земного радиуса.

Так как расстояние до Луны в 60⅓ раза больше экваториального радиуса Земли, а ее полудиаметр равен 1:3⅔ или 0,273 полудиаметра Земли, мы видим, что Гиппарх имел очень верное представление о размере и удаленности нашей ближайшей небесной соседки [165]. Проблема нахождения расстояния до

Солнца (и, следовательно, его истинного размера) находилась вне досягаемости инструментальных возможностей астрономов до изобретения телескопа, однако это делает большую честь Гиппарху, что, приступив к проблеме с разных сторон, он понял, что ее придется оставить неразрешенной. С другой стороны, Птолемей, определив лунный параллакс путем сравнения зенитных расстояний с теми, которые вытекали из его теории, сделал явный шаг назад, когда вывел расстояние до Солнца из лунных затмений, что практически идентично результату, следующему из найденной Аристархом пропорции; и в течение полутора тысяч лет астрономы без лишних вопросов принимали его солнечный параллакс, равный 2′51″. Он использовал следующие данные («Синтаксис», Y, 15—16, с. 425—426):

1210 [166]

5,5 [167]

Интересно, однако, отметить, что Гиппарх не единственный астроном своей эпохи, осознавший, что Солнце не в 20 раз, а намного, гораздо дальше Луны. Достойную упоминания попытку определить фактический размер Солнца, основанную на смелой гипотезе относительно его расстояния, предпринял Посидоний, о чем сообщают нам Клеомед (II, 1) и Плиний (II, 85). Посидоний, опираясь на Эратосфена, знал, что в Сиене, под тропиком Рака, в области диаметром 300 стадиев в момент, когда Солнце находится в созвездии Рака, в полдень не видно теней. То есть на любую точку в пределах этой области падают прямые лучи Солнца в направлении перпендикулярном поверхности Земли, и, так как любой перпендикуляр к поверхности сферы проходит через ее центр, Посидоний заключил, что конус с вершиной в центре Земли и основанием в видимом диске Солнца отсекает от поверхности

Земли круг диаметром 300 стадиев. Если допустить, что орбита Солнца в 10 000 раз больше окружности Земли, то диаметр Солнца в 10 000 раз больше диаметра площади, в которой предметы не отбрасывают тени. Если теперь мы спросим, какой радиус Земли предположил Посидоний, ответ мы найдем в следующих цифрах у Плиния, который, вероятно, взял их из своего обычного источника – Теренция Варрона. Согласно Плинию, Посидоний предположил, что расстояние от поверхности Земли до области облаков и ветров составляет 40 стадиев, оттуда (inde) начинается ясный и прозрачный воздух, полный безмятежного света, но между облачной областью и Луной находится пространство в 2 000 000 стадиев, а оттуда (inde) до Солнца – 500 000 000 стадиев, «и только благодаря такому расстоянию Солнце при своем громадном размере не сжигает Землю». Если соединить это с утверждением Клеомеда, что диаметр Солнца равен 10 000 × 300 стадиев, то простой подсчет дает радиус Земли 50 205,02 стадия. Но текст у Плиния явно подвергся искажению, так как нет никакого смысла в предположении, что расстояние от поверхности Земли до Солнца равно 502 000 040 стадиев, ведь использовались только круглые числа. Нет никаких сомнений, что второе inde следует вычеркнуть и Посидоний просто высчитал расстояние до Солнца от центра Земли, равное 500 000 000 стадиев, и радиус Земли, равный одной десятитысячной части расстояния, то есть 50 000 стадиев. Таким образом, в округленных числах окружность составит 300 000 стадиев, или ровно в 1000 раз больше области без тени. Тот факт, что Посидоний не принял величину окружности Земли 240 000 стадиев, которую вычислил сам, а использовал гораздо более старую величину 300 000 стадиев, нужно считать еще одним доказательством того, что он хотел оперировать только круглыми числами. Аналогичным образом, видимый диаметр Солнца стал 360° : 1000, хотя он и знал, что 360°: 720 намного ближе к истине. По сути дела, он следовал по пятам за Архимедом, который в своем «Исчислении песчинок» стремился мысленно образовать самую большую сферу, какую только можно себе представить, наполнить ее песчинками, пересчитать их и затем доказать, что всегда можно представить себе число еще больше. С этой целью Архимед произвольно предположил, что длина окружности Земли равна 3 000 000 стадиев, а длина окружности орбиты Солнца в 10 000 раз больше. Посидоний взял у него второе число, показав тем самым, что не верит в большой параллакс и, следовательно, малое расстояние до Солнца, хотя этого мнения придерживались все астрономы Античности, за исключением Гиппарха.