Карл Гильзин - Путешествие к далеким мирам
- Название:Путешествие к далеким мирам
- Автор:
- Жанр:
- Издательство:Государственное издательство детской литературы Министерства просвящение РСФСР
- Год:1960
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Карл Гильзин - Путешествие к далеким мирам краткое содержание
В книге рассказывается о том, как создавалась астронавтика — наука о межпланетных сообщениях, об основах этой науки, ее удивительном настоящем и увлкательном будущем. В ней говорится о многочисленных невиданных трудностях, стоящих на пути человека в Космос, и о том, как наука и техника преодолевают эти трудности, как готовится полет человека в космическое пространство.
Путешествие к далеким мирам - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Воспользуемся формулой V = 2,3· C ·lg m .
15 = 2,3·2,5·lg m ; lg m = 2,6; m ≈400.
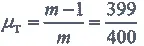
то есть вес топлива составляет 99,75 процента взлетного веса ракеты.
Такую ракету построить нельзя.
2. Отношение масс ракеты m= 10. Какова должна быть скорость истечения газов, чтобы ракета достигла скорости 8 км/сек?
Воспользуемся формулой V = 2,3· C ·lg m .
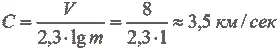
Такую скорость истечения можно получить с помощью высококалорийных топлив.
II. ФОРМУЛА ДЛЯ ОПРЕДЕЛЕНИЯ КОНЕЧНОЙ СКОРОСТИ СОСТАВНОЙ (МНОГОСТУПЕНЧАТОЙ) РАКЕТЫ
Если составная ракета состоит из n ступеней, а скорость истечения газов из двигателей всех ступеней одинакова и равна С , то конечная скорость последней ( n -й) ступени
где m 1· m 2… m n — отношения масс отдельных ступеней ракеты (1-й, 2-й… n -й), представляющие собой отношение начальной массы каждой ступени (включающей массу всех последующих ступеней в качестве полезной нагрузки) к этой же массе за вычетом массы топлива, запасенного на данной ступени.
Допустим, что ракета состоит из двух ступеней со следующими весовыми данными:
1-я ступень: вес ракеты — 2000 кг, вес топлива — 8000 кг;
2-я ступень: вес ракеты — 400 кг, вес топлива — 1600 кг.
Скорость истечения газов из двигателей обеих ступеней одинакова и равна С = 2500 м/сек.
Какова будет конечная скорость второй ступени ракеты?
По вышеприведенной формуле
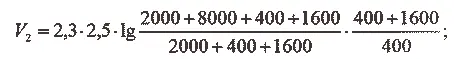
Если бы ракета была не составной и имела такое же количество топлива, то ее конечная скорость была бы
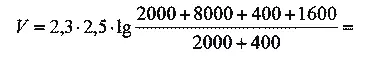
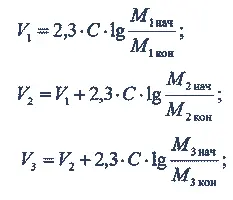
Но тогда V 3 = 2,3· C ·lg m 1 + 2,3· C ·lg m 2 + 2,3· C ·lg m 3 = 2,3· C ·lg( m 1· m 2· m 3).
III. ФОРМУЛА ТЯГИ РЕАКТИВНОГО ДВИГАТЕЛЯ
Эта формула позволяет определить величину тяги реактивного двигателя любого типа. Формула получается на основе закона механики (следствие второго закона Ньютона), по которому изменение количества движения тела равно действующей на него силе (в единицу времени).
Для ракетного двигателя
где R — сила тяги в кг ;
М — масса газов, вытекших из двигателя за секунду (масса равна секундному весовому количеству газов, деленному на ускорение земного тяготения, то есть где G сек — в кг/сек
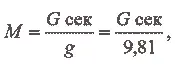
С — скорость истечения газов в м/сек .
Для воздушно-реактивных двигателей формула для тяги иная, так как изменение скорости воздуха, проходящего через двигатель, равно
где V — скорость полета; добавкой топлива к воздуху обычно пренебрегают, так как она относительно невелика. Поэтому в случае воздушно-реактивного двигателя
1. В пороховой ракете сгорает 1 кг пороха в секунду. Газы вытекают со скоростью 1200 м/сек. Какую тягу развивает двигатель?
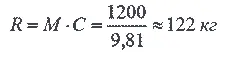
2. На реактивном истребителе установлен турбореактивный двигатель, через который в полете со скоростью 1440 км/час протекает 120 кг воздуха в секунду. С какой скоростью вытекают при этом газы из двигателя, если его тяга равна 6 т?
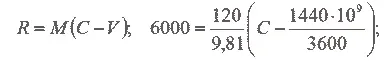
IV. ФОРМУЛА, СВЯЗЫВАЮЩАЯ СКОРОСТЬ ИСТЕЧЕНИЯ ГАЗОВ С ТЕПЛОТВОРНОСТЬЮ ТОПЛИВА
Скорость истечения газов из сопла ракетного двигателя зависит от теплотворности применяемого топлива и степени совершенства двигателя:
где С макс. — максимальная теоретическая скорость истечения в м/сек ,
Н — теплотворность топлива, то есть количество тепла, выделяющегося при сгорании 1 кг топлива (измеряется в ккал/кг ).
Значит, скорость истечения изменяется пропорционально корню квадратному из теплотворности топлива.
На сколько увеличится теоретическая скорость истечения газов при переходе с пороха, имеющего теплотворность 1000 ккал/кг , на жидкое топливо (керосин + жидкий кислород) с теплотворностью 2400 ккал/кг?
C пороха = 91,5√1000 = 2890 м/сек,
C ж. топл. = 91,5√2400 = 4490 м/сек,
Конечно, истинные скорости истечения из-за различных потерь в двигателе будут иными, значительно меньшими (для пороха 1400–1800 м/сек , для жидкого топлива 2200–2500 м/сек ).
В двигателе тепловая энергия топлива преобразуется в кинетическую энергию вытекающих газов. Если это преобразование происходит без потерь, то по закону сохранения энергии где А — тепловой эквивалент работы;
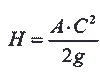
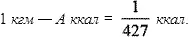
Следовательно, С =√2 gH/A = √2·9,81·427 Н ≈ 91,5√ Н
V. ФОРМУЛА, СВЯЗЫВАЮЩАЯ СКОРОСТЬ ИСТЕЧЕНИЯ С ПАРАМЕТРАМИ ГАЗОВ В ДВИГАТЕЛЕ
Влияние топлива на скорость истечения непосредственно сказывается через параметры газов в двигателе. Эта зависимость дается формулой где Т — абсолютная температура газов в камере сгорания двигателя;
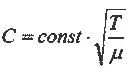
μ — молекулярный вес продуктов сгорания;
const — приближенно постоянная величина для данного двигателя и данных условий его работы (точнее, она несколько зависит и от состава продуктов сгорания).
Значит, скорость истечения газов прямо пропорциональна корню квадратному из абсолютной температуры газов и обратно пропорциональна корню квадратному из молекулярного веса газов.
Читать дальшеИнтервал:
Закладка:









