Карл Гильзин - Путешествие к далеким мирам
- Название:Путешествие к далеким мирам
- Автор:
- Жанр:
- Издательство:Государственное издательство детской литературы Министерства просвящение РСФСР
- Год:1960
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Карл Гильзин - Путешествие к далеким мирам краткое содержание
В книге рассказывается о том, как создавалась астронавтика — наука о межпланетных сообщениях, об основах этой науки, ее удивительном настоящем и увлкательном будущем. В ней говорится о многочисленных невиданных трудностях, стоящих на пути человека в Космос, и о том, как наука и техника преодолевают эти трудности, как готовится полет человека в космическое пространство.
Путешествие к далеким мирам - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
L ап, L пер., — расстояния апогея и перигея от центра Земли (в задаче L 2, L 1).
Это соотношение непосредственно вытекает из закона сохранения момента количества движения.
Так как L ап = L 2 = 6,6; L пер = 1 и V пер.= V 1 = 10,4 км/сек , то
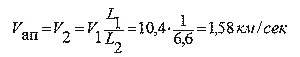
Точно так же в предыдущей задаче
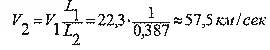
4. Какова будет скорость советской искусственной планеты в ее движении вокруг Солнца?
По предварительным сведениям, опубликованным в советской печати, наибольшее расстояние новой планеты от Солнца будет равно 197,2 миллиона километров, а наименьшее — 146,4 миллиона километров. Следовательно, большая ось орбиты будет равна 343,6 миллиона километров.
Но тогда и максимальная скорость планеты (в перигелии):
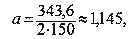
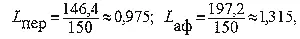
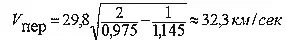
а минимальная скорость (в афелии):
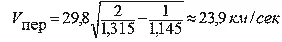
VI. ПРОДОЛЖИТЕЛЬНОСТЬ ПОЛЕТА ПО ЭЛЛИПТИЧЕСКОЙ ОРБИТЕ
При движении по эллипсу вокруг Солнца продолжительность полного обращения может быть определена с помощью третьего закона Кеплера, по которому квадраты времен обращения планет относятся как кубы их средних расстояний от Солнца (то есть кубы больших полуосей эллиптических орбит):
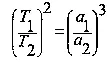
где Т — продолжительность одного обращения;
а — большая полуось эллиптической орбиты.
Проще всего производить сравнение с периодом обращения Земли, равным, как известно, одному году, или 365 суткам. Тогда
где Т — в сутках, а — в астрономических единицах.
При движении вокруг Земли период обращения можно сравнивать с периодом обращения кругового спутника у самой поверхности, то есть на высоте Н = О . Этот период равен, как указывалось выше, 5070 секундам.
Поэтому
где Т — в секундах,
а — в радиусах земного шара.
1. Какова продолжительность полета корабля с Земли до Меркурия по наивыгоднейшему касательному полуэллипсу?
Период обращения по наивыгоднейшему эллипсу
Продолжительность полета
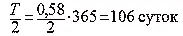
2. Какова продолжительность полета грузовой ракеты с Земли до суточной орбиты по касательному полуэллипсу (сопротивлением воздуха и активным участком траектории пренебрегаем)?
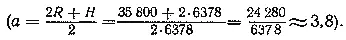
Продолжительность полета
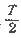
= 18 800 секунд, или ≈5,2 часа.
3. Какова продолжительность полета на Луну по наивыгоднейшему касательному полуэллипсу?
В этом случае поэтому Т = 5070 · 30,6 3/2 ≈ 860 000 секунд, или около 240 часов.
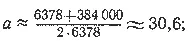
Продолжительность полета
≈ 120 часов (5 суток).
4. Какова величина больших полуосей орбит советских искусственных спутников?
В начале движения периоды обращения советских искусственных спутников равнялись:
первого спутника
второго спутника
третьего спутника
По формуле Т = 5070 3/2 находим:
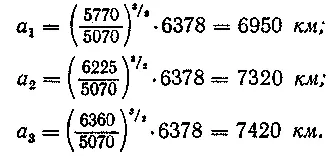
Истинные величины больших полуосей отличаются от приведенных выше приближенных, которые даны лишь в качестве иллюстрации.
5. Каков период обращения советской искусственной планеты, запущенной 2 января 1959 года?
Так как для этого случая а =1,145 (см. выше), то
что соответствует данным, опубликованным в советской печати.
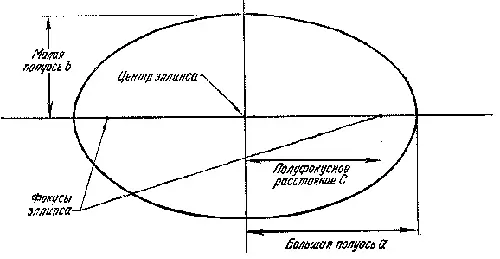
VII. ФОРМА ЭЛЛИПТИЧЕСКОЙ ОРБИТЫ
Для определения эллиптической орбиты, помимо величины большой полуоси, необходимо знать еще один из элементов орбиты — малую полуось b , полуфокусное расстояние с или эксцентриситет е . Эти величины связаны следующими соотношениями:
полуфокусное расстояние
эксцентриситет
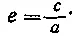
Для искусственных спутников Земли очевидны также следующие соотношения:
средняя высота спутника над Землей
или где H ап. — высота апогея орбиты;
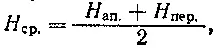
H пер.— высота перигея орбиты;
полуфокусное расстояние орбиты
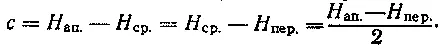
1. Определить элементы орбит советских искусственных спутников Земли по известным высотам апогея и перигея.
В соответствии с опубликованными данными примем следующие округленные значения для высот апогея и перигея советских искусственных спутников Земли:
H пер. = 225 км (для всех трех спутников); [146]
H ап.1 = 950 км, H ап.2 = 1670 км, H ап.3 = 1880 км .
Тогда средние высоты спутников над Землей будут равны:
для первого спутника H ср1 =
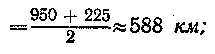
для второго спутника H ср2 =
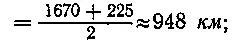
для третьего спутника H ср3 =
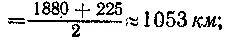
а полуфокусные расстояния соответственно:
Читать дальшеИнтервал:
Закладка:









