Карл Гильзин - Путешествие к далеким мирам
- Название:Путешествие к далеким мирам
- Автор:
- Жанр:
- Издательство:Государственное издательство детской литературы Министерства просвящение РСФСР
- Год:1960
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Карл Гильзин - Путешествие к далеким мирам краткое содержание
В книге рассказывается о том, как создавалась астронавтика — наука о межпланетных сообщениях, об основах этой науки, ее удивительном настоящем и увлкательном будущем. В ней говорится о многочисленных невиданных трудностях, стоящих на пути человека в Космос, и о том, как наука и техника преодолевают эти трудности, как готовится полет человека в космическое пространство.
Путешествие к далеким мирам - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
На сколько изменится скорость истечения газов из жидкостного ракетного двигателя, если температура в нем увеличится с 2500 до 3000°К, а молекулярный вес газов уменьшится с 18 до 14?
По приведенной выше формуле
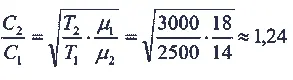
Значит, скорость истечения увеличится на 24 процента.
Раздел второй
ОСНОВНЫЕ ФОРМУЛЫ ДВИЖЕНИЯ В ПОЛЕ ТЯГОТЕНИЯ
I. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ НЬЮТОНА
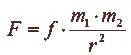
где F — сила притяжения между двумя небесными телами;
f — константа тяготения (гравитационная постоянная),
m 1, m 2 — массы притягивающихся тел;
r — расстояние между центрами тяжести этих тел.
Какая сила притяжения больше и на сколько — Луны и Солнца или Луны и Земли?
Сила притяжения Луны и Солнца:
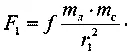
Сила притяжения Земли и Луны:
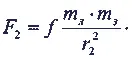
Очевидно,
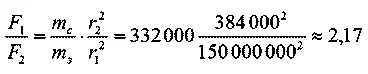
Значит, Луна притягивается Солнцем примерно вдвое сильнее, чем Землей.
Вес тела и ускорение земного тяготения изменяются обратно пропорционально квадрату расстояния от центра Земли:
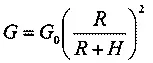
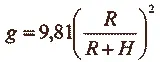
Здесь G и g — соответственно вес тела и ускорение земного тяготения на высоте Н над Землей;
R — радиус земного шара ( R — 6378 км);
G 0 — вес тела у земной поверхности.
На сколько уменьшатся вес и ускорение земного тяготения на высоте орбиты спутника, равной 800 км?
Изменение веса:
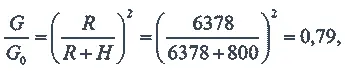
то есть вес уменьшится на 21 процент.
На столько же уменьшится и ускорение земного тяготения, то есть g = 9,81·0,79 = 7,75 м/сек 2.
II. ИСКУССТВЕННЫЙ СПУТНИК ЗЕМЛИ НА КРУГОВОЙ ОРБИТЕ
А. Круговая скорость
Как найти величину круговой скорости, то есть той скорости, с которой должен двигаться спутник, чтобы его высота над Землей оставалась неизменной?
Высота спутника не меняется в том случае если он каждое мгновение на столько же удаляется от Земли в своем движении по инерции, на сколько приближается к ней в результате непрекращающегося падения на Землю. Это и позволяет найти необходимую круговую скорость спутника.
Рассмотрим движение спутника за 1 секунду, причем для простоты будем считать, что спутник движется у самой поверхности Земли, то есть высота равна нулю. Тогда за 1 секунду спутник приблизится к центру Земли, в результате притяжения к ней, на величину
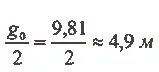
На эту же величину он должен удалиться от центра Земли, что позволяет построить прямоугольный треугольник (см. рисунок).
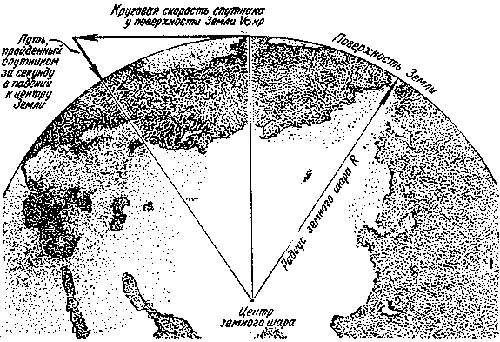
По теореме Пифагора
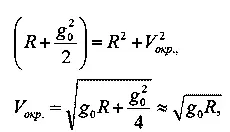
Эту же задачу можно решить и иначе. Если высота спутника не меняется, то это значит, что его центростремительное ускорение в точности равно ускорению земного тяготения. (Это вовсе не означает, как иногда пишут, что центробежная сила «уравновешивает» вес спутника.)
Следовательно,
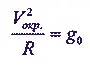
и
как и ранее.
Очевидно; на высоте Н
Но так как то
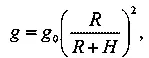
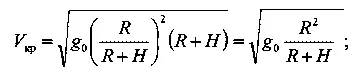
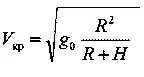
Это значит, что круговая скорость изменяется обратно пропорционально корню квадратному из расстояния до центра Земли.
| Высота Н в км | Круговая скорость Vкр. в м/сек |
|---|---|
| 0 | 7 910 |
| 255 | 7 760 |
| 1 000 | 7 360 |
| 1 670 | 7 040 |
| 35 800 | 3 080 |
| 384 000 (орбита Луны) | 1 010 |
Б. Период обращения спутника
Время, за которое спутник совершит один полный оборот вокруг Земли, равно, очевидно, длине пути за оборот, деленной на круговую скорость:
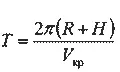
( Т — так называемый сидерический, или звездный, период обращения).
Но вследствие чего
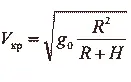
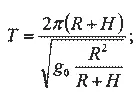
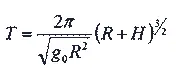
Подстановка значений R и g 0 дает следующую довольно точную для приближенных расчетов формулу:
| Высота Н в км | Период обращения спутника Т в сек |
|---|---|
| 0 | 5 070 (1,4 часа) |
| 255 | 5 400 (1,5 часа) |
| 1 000 | 6 340 (1,76 часа) |
| 1 670 | 7 200 (2 часа) |
| 35 800 | 86 400 (24 часа) |
| 384 000 | 2,36·10 6 (27,3 суток) |
III. СКОРОСТЬ ОТРЫВА (ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ)
Скорость отрыва (или параболическая скорость) есть та скорость, которая должна быть сообщена телу у поверхности Земли, чтобы полностью преодолеть поле земного тяготения — удалить тело в бесконечность.
Читать дальшеИнтервал:
Закладка:









