Карл Гильзин - Путешествие к далеким мирам
- Название:Путешествие к далеким мирам
- Автор:
- Жанр:
- Издательство:Государственное издательство детской литературы Министерства просвящение РСФСР
- Год:1960
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Карл Гильзин - Путешествие к далеким мирам краткое содержание
В книге рассказывается о том, как создавалась астронавтика — наука о межпланетных сообщениях, об основах этой науки, ее удивительном настоящем и увлкательном будущем. В ней говорится о многочисленных невиданных трудностях, стоящих на пути человека в Космос, и о том, как наука и техника преодолевают эти трудности, как готовится полет человека в космическое пространство.
Путешествие к далеким мирам - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Величина скорости отрыва V отр. определяется тем, что кинетическая энергия тела должна в этом случае в точности равняться работе преодоления поля тяготения; с помощью высшей математики получаем:
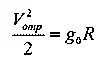
то есть работа полного преодоления поля земного тяготения равна работе поднятия тела при постоянном ускорении силы тяжести, равном его значению у земной поверхности g 0, на высоту земного радиуса R .
Так как √g 0R есть круговая скорость, то скорость отрыва V отp. в 1,41 раза больше круговой скорости:
| Высота Н в км | Скорость отрыва У отр. в км/сек |
|---|---|
| 0 | 11,2 |
| 300 | 10,9 |
| 1 000 | 10,4 |
| 1 670 | 9,9 |
| 35 800 | 4,3 |
| 384 000 | 1,42 |
IV. ОБЩИЙ ЗАКОН ДВИЖЕНИЯ КОСМИЧЕСКОГО КОРАБЛЯ В ПОЛЕ ТЯГОТЕНИЯ ОДНОГО НЕБЕСНОГО ТЕЛА
Примеры движения по кругу или по параболе, о которых шла речь выше, являются лишь частными случаями движения тела в поле тяготения небесного тела большой массы. Как известно из небесной механики, в общем случае орбитой такого движения является одна из кривых второго порядка (так называемых конических сечений): круг, эллипс, парабола или гипербола. Общий закон этого движения дается следующей формулой (так называемое уравнение живых сил, упрощенное для случая космического корабля, то есть тела небольшой массы):
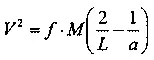
или где V — скорость движения тела массы пренебрежимо малой по сравнению с М ;
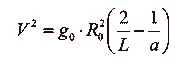
М — масса небесного тела;
f — гравитационная постоянная;
L — расстояние до центра тяжести небесного тела;
а — большая полуось орбиты;
g 0 — ускорение силы тяжести на поверхности небесного тела на расстоянии R 0 от его центра.
Как видно из формул, характер орбиты зависит лишь от величины, но не направления скорости V . Различные типы орбит соответствуют следующим частным случаям:
а) а = ∞ ,
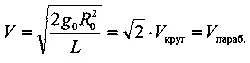
орбита — парабола;
б) а > ◯, V < V параб., орбита — эллипс;
в) L = а, V = V круг =
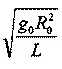
частный случай эллиптической орбиты — круговая;
г) а < ◯, V > V параб., орбита — гипербола (V гиперб.).
По какой орбите будет двигаться космический корабль, летящий на расстоянии 100 000 км от центра Земли со скоростью 5 км/сек?
По формуле откуда a ≈ — 24 000;
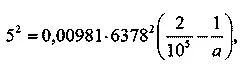
так как а < ◯, то V = V гиперб., орбита — гипербола.
V. ЭЛЛИПТИЧЕСКИЕ ОРБИТЫ
Наиболее важными для астронавтики являются эллиптические орбиты, по которым будут двигаться не только все новые искусственные спутники Земли, но чаще всего и космические корабли. Полет по гиперболической орбите — дело более отдаленного будущего (советская космическая ракета, запущенная 2 января 1959 года, летела в поле земного тяготения по гиперболе, а вокруг Солнца движется по эллипсу).
Формулы расчета эллиптических орбит могут быть получены из приведенного выше уравнения живых сил путем упрощений;
для движения вокруг Солнца:
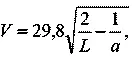
где V — в км/сек ,
L,a — в астрономических единицах (1 а. е. — расстояние от Земли до Солнца, равное примерно 150·10 6 км );
для движения вокруг Земли:
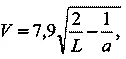
где V — в км/сек ,
L, а — в радиусах земного шара.
1. Какова должна быть скорость корабля при взлете с Земли для того, чтобы он смог совершить полет на Меркурий по наивыгоднейшей, то есть касательной, эллиптической орбите?
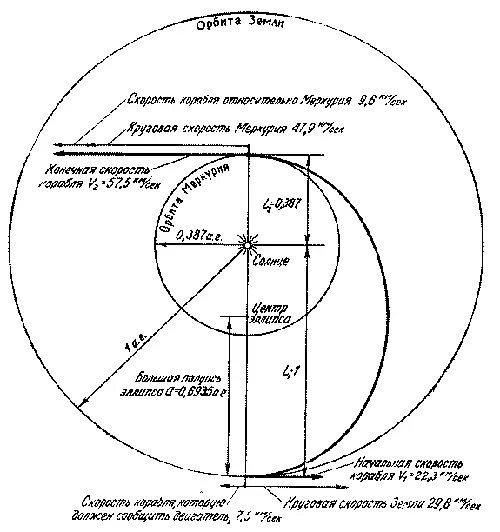
В этом случае
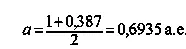
и
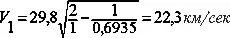
Так как круговая скорость Земли равна 29,8 км/сек , то, очевидно, кораблю при взлете нужно сообщить скорость против направления движения Земли по орбите, равную 29,8 — 22,3 = 7,5 км/сек .
2. Какова будет скорость корабля в упомянутой выше задаче на орбите Меркурия?
В этом случае L 2=0,387 а. е., а = 0,6935 а. е., вследствие чего
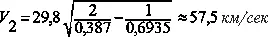
Так как круговая скорость Меркурия равна 47,9 км/сек (это можно проверить и так — она равна круговой скорости Земли, деленной на √0,387, то есть то корабль будет двигаться быстрее Меркурия на величину 57,5 — 47,9 = 9,6 км/сек .
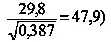
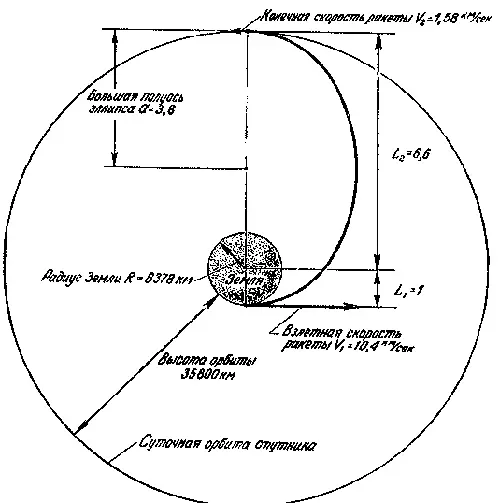
3. Какова должна быть взлетная скорость ракеты, доставляющей о Земли груз на искусственный спутник, находящийся на суточной орбите (высота 35 800 км), если сопротивление воздуха не учитывать? Какова будет скорость этой ракеты на орбите спутника?
В этом случае
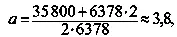
При взлете L 1 = 1, поэтому
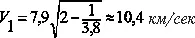
На орбите поэтому
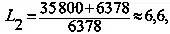
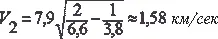
Примечание. Для решения этой задачи можно воспользоваться соотношением, связывающим величины скоростей в апогее и перигее эллиптической орбиты:
где V ап., V пер.— соответственно скорости движения в апогее и перигее (в задаче V 2, V 1);
Читать дальшеИнтервал:
Закладка:









