Вадим Романов - Прикладные аспекты аварийных выбросов в атмосферу

Плотность паровоздушной смеси записывается в виде [33]:

р = р в(1–0,608 F + F 1+ с),

где с — удельная концентрация дымового аэрозоля.

Плотность сухого воздуха р вудовлетворяет уравнению состояния

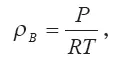
где Р — давление, Т — температура, R — газовая постоянная для воздуха.

Удельная влажность F m, при которой водяной пар в воздухе достигает насыщения, определяется из уравнения:

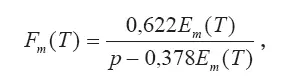
где

E m(T) — парциальное давление насыщенного водяного пара (Н/м 2), определяемое по формуле Магнуса [34]:

E m(T) = 610 ехр α(Т),

а(Т) =17,27(Т — 273,16)/(T — 35,86).

Формирование и подъем конвективной колонки дымового аэрозоля рассматривается в рамках односкоростной и однотемпературной модели дисперсной среды, применение которой правомерно, так как размеры дисперсных частиц (дым, пар, капли) намного превышают характерные молекулярно-кинетические пробеги, а время их скоростной и температурной релаксации значительно меньше времени развития конвективных движений. Кроме того предполагается малое объемное содержание дисперсной фазы, не учитываются эффекты столкновения частиц, коагуляция, образование дождевых капель и их выпадение.

Начало цилиндрической системы координат г, z выбирается в центре пожара на поверхности земли. Тогда система уравнений Навье-Стокса, определяющая развитие конвективных движений среды при пожаре, имеет следующий вид:

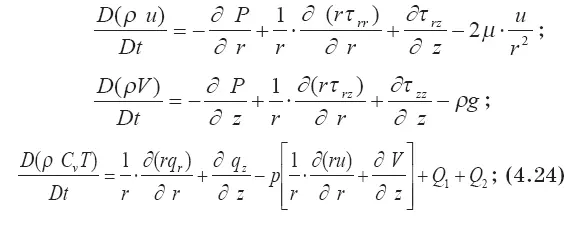
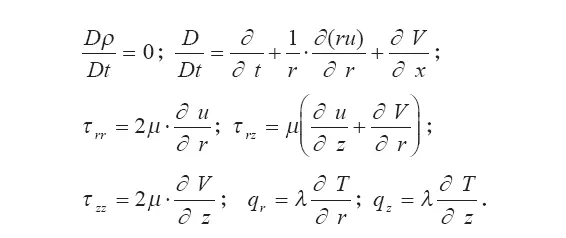
В этих соотношениях: u, V — радиальная и вертикальная составляющая скорости; C v— теплоемкость газа при постоянном объеме; g — ускорение свободного падения; μ, λ — коэффициенты динамической вязкости и теплопроводности.

Распространение мелкодисперсного дымового аэрозоля, перенос пара и влаги в виде капель описывается уравнениями турбулентной диффузии

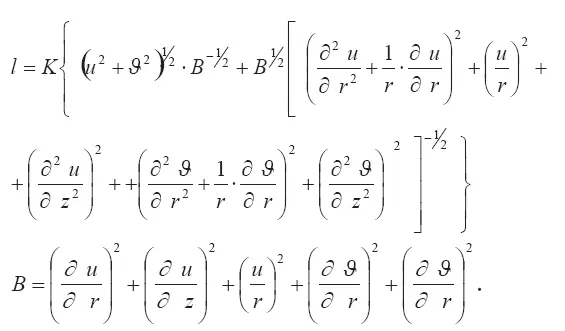
В этих соотношениях: μ е, μ t— коэффициенты ламинарной и турбулентной вязкости; l — длина пути перемешивания; К — эмпирическая константа.

Эффективные коэффициенты переноса предполагаются связанными соотношением

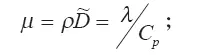
числа Рейнольдса и Шмидта равны Re=Sc.

Здесь: С p= γ · C v; γ — показатель адиабаты.

Начальное состояние атмосферы до пожара считается невозмущенным, т. е. при t = 0:

u = V = 0; T=T a(z);p=p a(z);F = F a(z);F 1= C = 0.

Распределение метеопараметров по высоте определялось в соответствии с моделью международной стандартной атмосферы и уравнением гидростатического равновесия [34]:

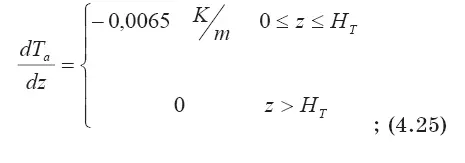
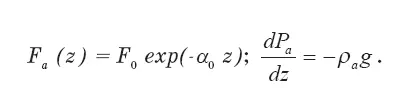
В этих соотношениях: p a(z) — плотность невозмущенной атмосферы; Н т— высота тропопаузы (10 ÷16 км); F 0— значение удельной влажности у поверхности земли;

а 0= 0,42 ч-0,84 км 1.

Пограничные условия на оси течения записываются в соответствии с симметричностью течения, поверхность земли считается адиабатичной и непроницаемой:

при r=0:

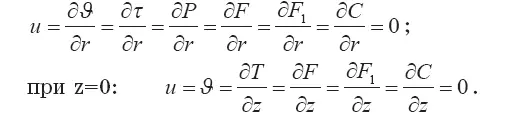
На внешних границах расчетной области принимались условия отсутствия градиентов скоростей и давлений; для входящего в область колонки потока считалось, что Т = T a(z), F = F a(z), F 1= С = 0; для выходящего потока — градиенты температуры, удельной влажности и концентрации брались нулевыми.

Численное решение изложенной модели показало, что в процессе развития в атмосфере конвективная колонка проходит несколько стадий: формирование, подъем и зависание.

На Рис. 4.2 представлена рассчитанная картина процесса формирования дымового облака над пожаром в последовательные моменты времени (показаны изолинии 4-х различных концентраций аэрозоля: с х, с 2, с 3, с 4).

На начальной стадии формирования колонки (t < 1000 с) движение влажного воздуха происходит без фазовых превращений. На границе пожара возникает интенсивный тороидальный вихрь, способствующий более быстрому подъему аэрозольных частиц по периметру очага горения (Рис. 4.2а).

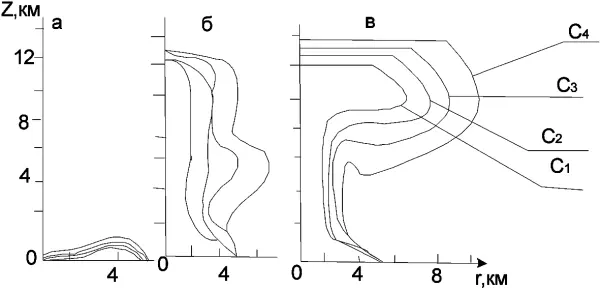
Рис. 4.2. Динамика формирования облака аэрозольных частиц над пожаром: R = 5 км; q m= 5 10 4Вт/м 2в моменты времени: а) 900 с; б) 1800 с; в) 2700 с.

В дальнейшем по мере увеличения мощности тепловыделения формируется устойчивый, направленный к центру пожара поток газа. Окружающий зону пожара воздух втекает в нее, нагревается и вместе с продуктами горения поднимается вверх, образуя вертикально направленный поток — тепловую колонку. Поднимающийся в восходящей струе влажный воздух достигает уровня конденсации (на высотах > 3 км), что приводит к дополнительному подъему аэрозолей (рис. 4.26).

Тороидальный вихрь, образовавшийся при малых временах на периферии пожара, под действием сил плавучести поднимается, формируя характерную грибовидную форму (рис. 4.2в) — стадия зависания колонки.

Расчеты показали, что при мощности пожара q m= 5-10 4Вт/м 2наибольшая вертикальная скорость потока (43 м/с) наблюдается на оси симметрии, при этом максимальная величина радиальной скорости у границ очага горения не превышает 17 м/с. Вовлечение холодного воздуха в восходящую струю наблюдается до высоты «4 км. На высотах от 7 до 11 км образуется зона зависания, в которой дымовой аэрозоль и вовлеченный в струю воздух растекаются в горизонтальном направлении от оси симметрии течения. Через 1 час дымовое облако растекается на площади 700 км 2, что почти на порядок больше площади очага горения.

Вода, выделяющаяся при конденсации влажного воздуха, в виде дождевых капель, снега и льда может выпасть в виде осадков.

Полученные результаты показывают, что динамика формирования конвективной колонки, высота подъема аэрозоля и характер его распределения в выбросе зависят не только от мощности пожара, но и от влажности атмосферы. Фазовые переходы, вызванные присутствием влаги в атмосфере, существенно влияют на характеристики подъема, зависания и выноса аэрозоля в атмосферу, а также процессы вымывания осадками частиц аэрозоля. В связи с этим при анализе пространственно-временной картины формирования тепловой колонки при пожарах необходим учет влажности и устойчивости атмосферы, а также уровня тропопаузы.