Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Да, дождь не падает крупными каплями… Но, к сожалению, бывает крупный град! Размер градин значительно увеличивается, если они попадают в несколько последовательных восходящих течений. В настоящее время мало что можно сделать, чтобы предотвратить их образование; идея засеивать облака частицами, предназначенными активизировать образование капель, оказалась неудачной.

При возникновении капли в земных условиях ее росту больше некоторого критического размера препятствует гравитация. Рассмотрим, например, формирование капли в капельнице (илл. 3). При достаточном давлении на насадку из капельницы вытекает вода. Форма образующейся при этом капли отличается от сферы, однако во всех направлениях имеет один и тот же характерный размер R (илл. 3a). Таким образом, ее масса оказывается порядка ρ R 3(где ρ – плотность жидкости), а вес – порядка g ρ R 3(где g – ускорение свободного падения). Поверхностная энергия капли, как мы уже видели выше, при этом имеет порядок σ R 2, где σ – поверхностное натяжение жидкости. В некоторый момент времени под действием силы тяжести капля начинает отрываться от капельницы (илл. 3b). Пройдя путь порядка R , капля уменьшает гравитационную потенциальную энергию примерно на g ρ R 4 (изменение потенциальной энергии силы тяжести между двумя точками равно весу объекта, умноженному на разницу высот). Но в ходе этого процесса капля растянулась, ее поверхность увеличилась, и, соответственно, возросла примерно на σ R 2 ее поверхностная энергия. Капля под действием силы тяжести оторвется от капельницы только тогда, когда выигрыш в потенциальной энергии капли в поле тяжести превысит увеличение поверхностной энергии, то есть при условии, что радиус капли R превысит так называемую капиллярную длину R 1 :

Капля меньшего радиуса от капельницы не оторвется. Отвлекаясь от нашего эксперимента с капельницей, можно утверждать, что капиллярная длина является той гранью, за которой роль гравитации становится преобладающей по сравнению с поверхностной энергией. Например, если поместить совсем небольшое количество жидкости на ровную поверхность, то образуется капля, свободная поверхность которой будет практически сферической. Но если радиус зоны контакта с поверхностью приближается к величине R 1 , то капля деформируется и принимает все более плоскую форму. В заключение скажем, что радиус капель обычно не превышает значение R 1 (см. врезку на пред. с.). Для воды, при g = 9,8 м/с 2и ρ = 1000 кг⋅м 3, капиллярная длина составляет порядка 3 мм.

Бывают капли воды в воздухе и пузырьки воздуха в воде (см. главу 15, «Возникновение первых пузырьков»). Но можно создать и воздушные пузыри в воздухе – с помощью мыльного раствора воды! Он образует весьма устойчивые пузыри, которые невозможно было бы получить, используя чистую воду (илл. 4).

4. Мыльные пузыри. Прекрасные переливы цвета вызваны интерференцией (см. главу 3, «Мыльные пузыри»)

Молекулярная структура мыльной пленки – сама по себе урок физики. Мыло содержит так называемые поверхностно-активные вещества, молекулы которых характеризуются гидрофильной («любящей воду») головкой и гидрофобным («боящимся воды») хвостом. Чтобы удерживать головку в воде и хвосты вне воды, эти молекулы скапливаются у поверхности и выстраиваются перпендикулярно ей (илл. 5). Таким образом, присутствие молекул поверхностно-активного вещества в воде уменьшает коэффициент поверхностного натяжения раствора. Равновесная форма мыльного пузыря такая же, как и у небольшой капли. Это сфера, которая минимизирует поверхностную энергию системы. Поэтому неудивительно, что небольшие пузыри, как и маленькие капли, оказываются сферическими. Однако, в отличие от капель, сферическими часто могут быть даже большие пузыри. Дело в том, что мыльная пленка тонкая и чрезвычайно легкая, и поэтому воздействие гравитации на пузырь оказывается незначительным. Таким образом, мыльные пузыри отлично подходят для изучения поверхностного натяжения и его эффектов. Если бы размер пузыря регулировало только поверхностное натяжение, то оно бы неограниченно уменьшало его поверхность, пузырь становился бы все меньше и меньше и в конечном итоге исчезал. Но поскольку внутри пузыря находится воздух, то уменьшение диаметра приводит к росту давления внутри него, и, когда последнее достигает величины суммы атмосферного давления и дополнительного давления Лапласа стенок пузыря, устанавливается баланс сил.

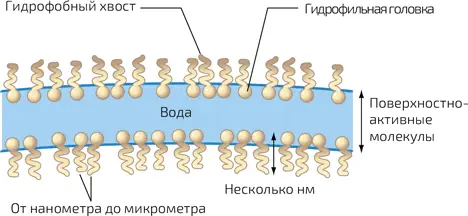
5. Схема мыльной пленки. Молекулы поверхностно-активного вещества уменьшают поверхностное натяжение воды и тем самым препятствуют уничтожению мыльного пузыря. Гидрофильная головка обычно обладает электрическим зарядом и поэтому сильнее взаимодействует с молекулой воды, которая обладает электрическим дипольным моментом (см. главу 16, илл. 5)

Откуда же берется избыточное давление Δ P , отличающее давление внутри мыльного пузыря от атмосферного? Для сферического мыльного пузыря радиусом R расчет прост. Поверхностная энергия равна произведению площади поверхности на поверхностное натяжение: S σ’ = 4π R 2σ’, где σ’ = 2σ, то есть вдвое превышает поверхностное натяжение мыльной жидкости, так как пленка имеет две стороны. Небольшое увеличение радиуса пузырька δ R приводит к изменению поверхности на величину 8π R δ R и, следовательно, к изменению энергии поверхности на 8πσ’ R δ R (илл. 6). Это изменение энергии должно компенсироваться работой сил давления, приложенных к стенкам пузырька при увеличении его радиуса (работа силы равна энергии, переданной системе этой силой в процессе перемещения). Эта работа равна избыточному давлению Δ P , умноженному на изменение объема пузыря, то есть 4π R 2δ R Δ P . Поэтому мыльный пузырь радиусом R пребывает в равновесии тогда, когда давление воздуха внутри превышает атмосферное на

Δ P = 2σ’ /R. (2)

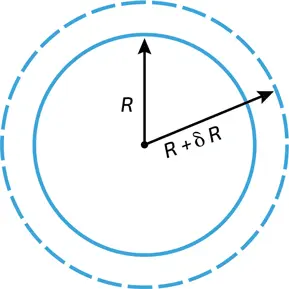
6. Изменение энергии, вызванное бесконечно малым расширением пузырька, должно быть равно нулю в состоянии равновесия