Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Δ P = σ’/ R . (3)

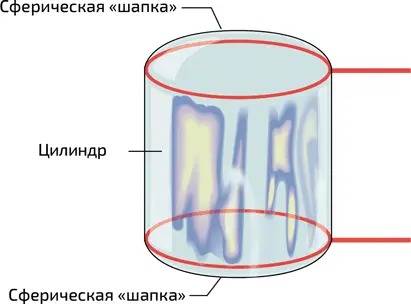
9. Цилиндрический мыльный пузырь, сформировавшийся между двумя кольцами. Две сферические «шапки» замыкают пузырь

«Шапки» пузыря при этом являются сферическими сегментами радиуса 2 R, который определяется формулами (2) и (3). А что произойдет, если они лопнут? При этом исчезнет перепад давления внутри и снаружи мыльной пленки. В результате пленка между двумя кольцами, для того чтобы минимизировать поверхностную энергию, перестает быть цилиндрической и деформируется (илл. 10). Получающаяся в результате такой деформации поверхность приобретает форму лошадиного седла и называется катеноидом. С математической точки зрения это поверхность, которая формируется вращением цепной линии вокруг оси (цепная линия, в свою очередь, – это кривая такой формы, какую принимает подвешенная между двумя точками цепочка, например колье). При изменении формы рамки, независимо от ее геометрии, поверхность, принимаемая пленкой, всегда будет соответствовать минимуму ее площади (такая поверхность называется минимальной) (см. главу 6, врезку «Кривизна, средняя кривизна, цепочка и катеноид»).

10. Поверхность, образованная мыльным пузырем между двумя параллельными кольцами, называется катеноидом. Любое его продольное сечение вогнутое, и любое поперечное сечение (окружность) – выпуклое

Оставим мыльные пузыри и вернемся к каплям, а точнее – ко всем знакомой ситуации: неплотно закрытый кухонный кран подтекает, роняя капли через регулярные промежутки времени (илл. 11). Их падение происходит очень быстро, и мы невооруженным глазом не можем различить детали – они доступны только высокоскоростной камере. Однако, и не имея такой камеры, бельгийский физик Жозеф Плато (1801–1883) в XIX веке сумел подробно проанализировать форму этих капель. Опытный экспериментатор решил устранить действие силы тяжести – тогда падающие капли будут двигаться достаточно медленно и за ними можно будет проследить невооруженным глазом. Вместо того чтобы ронять капли воды в воздухе, он использовал другую, не смешиваемую с водой, жидкость с плотностью, близкой к плотности воды (см. главу 6, врезку «Два эксперимента по следам Плато»). В этом случае действующая на капли выталкивающая сила Архимеда (глава 15) почти полностью компенсирует их вес. И все происходит так, как будто капли освободились от действия гравитации.

11. Неплотно закрытый кран подтекает. Динамика образования капель сложна. Ее детально изучали в 1990-х годах

Таким образом, Плато смог наблюдать образование капель на выходе из крана. Оказалось, что между формирующейся каплей и краном образуется жидкая нить, которая постепенно становится все тоньше, и утончается до тех пор, пока капля не отделится. Интересно, что при этом на нити образуется сопроводительная вторичная капля, видимая, например, на последней фотографии на илл. 3. Этот «спутник», систематически возникающий при образовании капель, стал открытием Плато. Опишем еще одну его находку.

При вытекании из крана тонкой струи видно, что она остается непрерывной и цилиндрической только в верхней части. Ниже струя теряет свою регулярную форму, и человеческий глаз не в состоянии различить, что с ней происходит далее (см. главу 6, врезку «Два эксперимента по следам Плато»). Но мы можем догадаться. Цилиндрическая форма соответствует относительно большой поверхностной энергии струи. Следовательно, в целях минимизации своей поверхностной энергии струя рассыпается на множество небольших капель (илл. 11). Цилиндрическая струя оказывается неустойчивой! Это явление называется «неустойчивость Рэлея – Плато», поскольку его теория была разработана лордом Рэлеем (см. главу 3, «Цвет неба в хорошую погоду»).

В каждой своей точке кривая (при определенных условиях непрерывности, дифференцируемости и т. д.) характеризуется радиусом кривизны R . Последний определяется как радиус окружности, наилучшим образом приближающей эту кривую в выбранной точке. Соответственно, в каждой точке кривой можно определить и величину ее кривизны γ = 1/ R .

В свою очередь, поверхность в любой точке A (см. илл.) характеризуется двумя радиусами кривизны: R 1 и R 2 . Они соответствуют минимальным и максимальным значениям радиуса кривизны при сечении поверхности в этой точке плоскостью, проходящей через нормаль. Радиус кривизны считается положительным, если кривая в сечении выпуклая, и отрицательным, если она вогнутая (на рисунке R 2 < 0 и R 1 > 0). Среднюю кривизну γ определяют посредством отношения 2γ = 1/ R 1 + 1/ R 2 .

Необходимым и достаточным условием для того, чтобы поверхность была минимальной, оказывается требование, чтобы ее средняя кривизна в любой точке поверхности была равной нулю, то есть два основных радиуса кривизны должны быть равными по модулю, но иметь противоположные знаки.

Существует большое разнообразие минимальных поверхностей. Однако особую роль среди них занимают катеноиды. Читатель, обладающий некоторыми знаниями о дифференциальном исчислении, без особого труда докажет, что уравнение цепной линии определяется выражением y = αch ( kx ). Вращение цепной линии вокруг оси x порождает катеноид, который имеет нулевую среднюю кривизну. Можно также доказать, что именно эта поверхность соответствует устойчивой форме мыльной пленки, заключенной между двумя параллельными кольцами, при условии что они находятся достаточно близко друг к другу (илл. 10). Если же их развести достаточно далеко, то катеноид лопнет и останется два диска внутри колец.

Если же давление по обе стороны мыльной пленки оказывается разным, то она образует поверхности со средней кривизной, равной во всех точках, но отличной от нуля. Скажем, таковы мыльные пузыри, возникшие на проволочной раме и удерживающие воздух. Простым примером такой поверхности является замкнутый двумя сферическими «шапками» цилиндрический пузырь (илл. 9): его средняя кривизна γ везде равна 1/(2 R ), где R – радиус колец.

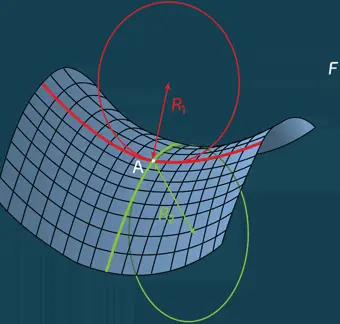
Геометрия минимальной поверхности (форма мыльной пленки, находящейся под равными давлениями со всех сторон). В любой точке A такой поверхности лежащие на ней кривые либо вогнуты (красная кривая), либо выпуклы (зеленая кривая). Красная кривая соответствует минимальной кривизне линии, уходящей вверх (вогнутой), а зеленая – минимальной кривизне линии, загибающейся вниз (выпуклой). Для минимальной поверхности обе кривизны 1/ R 1 и 1/ R 2 должны быть равны по модулю