Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Сначала рассмотрим поток тепла, поступающий в пиццу снизу, сквозь рабочую поверхность печи посредством механизма теплопроводности. Предположим, что нагреваемая пламенем ее внутренняя поверхность (илл. 3) имеет температуру T 2 = 330 °C. В месте, на которое укладывается пицца, верхняя граница кирпича ( под ) постоянно охлаждается холодным тестом, имеющим температуру T 0 = 10 °C, и, следовательно, ее температура T 3 должна быть ниже T 2 . Количество теплоты, передаваемой посредством теплопроводности за время t через рабочую поверхность S пицце, пропорционально разности температур ( T 2 – T 3 ) между ее нижней и верхней границами: Λ t ( T 2 – T 3 )/ d , где Λ – теплопроводность огнеупорного кирпича и d – толщина (см. врезку «Теплопроводность материалов»).

Допустим, что эта теплота идет только на нагрев пиццы. Тогда количество теплоты, полученной на единицу площади пиццы, составляет

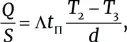
где t п время выпечки пиццы. По словам Антонио, оно составляет около 120 с. Теперь мы должны признаться, что не знаем точно, чему равна температура T 3 . Снова доверимся Антонио: по его мнению, она составляет около 200 °C. Зная, что толщина рабочей поверхности равна d = 2 см, а проводимость кирпича – Λ = 0,86 Вт⋅м –1K –1, получим

Q / S = 0,86 × 120 × 130/0,02 Дж/м 2, или 67 Дж/см 2.

Это количество теплоты, полученной за счет теплопроводности, значительно меньше общего тепла Q 0 / S = 190 Дж/см 2, рассчитанного ранее. Таким образом, ролью излучения в процессе приготовления пиццы пренебречь нельзя.

Выше мы говорили о передаче тепла посредством теплопроводности. Однако, когда курицу готовят на вертеле в электрической духовке, мясо вообще не касается горячих стенок. И все же оно запекается! В этом случае тепло курице передается частично излучением, которое испускают нагревательный элемент и стенки, а частично – посредством конвекции нагретого воздуха. Возвращаясь к объекту нашего интереса – пицце, мы обратимся к роли излучения.

4. Пиццы выпекаются в дровяной печи. Мастер виртуозно замешивает тесто, выкладывает на него начинку и ставит пиццу в печь

Теплопроводность – относительно медленный процесс, особенно в твердых телах. Механизм этого явления был проанализирован в начале XIX века Жозефом Фурье, о котором мы уже говорили в главе 7.

Если между двумя плоскими границами тела создана разность температур Δ T, а расстояние между ними Δ x , то тепловой поток ϕ, протекающий через поверхность площади S перпендикулярно ей, равен

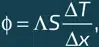
где поток ϕ измеряется в Вт, площадь S – в м 2, Δ T – в K, а Δ x – в м и где коэффициент Λ, называемый теплопроводностью материала, измеряется в Вт⋅м –1⋅K –1. Этот тепловой поток представляет собой то количество тепла, которое передается за единицу времени между двумя границами. Чем выше теплопроводность, тем больше тепловой поток и тем эффективнее материал проводит тепло.

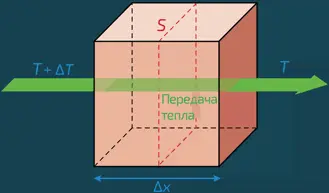
Теплопроводность через стенку толщины Δ x между двумя областями с температурами T и T + Δ T соответственно. Количество теплоты, передаваемое за время Δ t , равно

Кирпичная печь Антонио (илл. 4) имеет двойной теплоизолированный свод: его температура несколько выше, чем у рабочей поверхности печи, но для оценки мы примем и ее равной 330 °C (то есть 603 K). При этой температуре свод, как и боковые стенки, испускает электромагнитное, главным образом инфракрасное, излучение (см. главу 3, «Цветовое зрение»). Предполагая, что излучаемая мощность на единицу площади определяется законом Стефана – Больцмана (см. врезку «Закон Стефана – Больцмана»), получим

Q ´/( St ) = 5,67⋅10 –8× 603 4= 7 500 Вт⋅м –2.

Таким образом, в течение 120 секунд, пока пицца находится в печи, она получает на единицу поверхности теплоту Q ´/ S = 7500 × 120 ≈ 900 кДж⋅м –2, или 90 Дж⋅см –2.

Кратко подведем итог: общее количество теплоты Q 0 , подаваемое в пиццу, с одной стороны, обеспечивается теплопроводностью, а с другой – излучением, то есть Q 0 = Q + Q ´ (илл. 5). Сложив 68 Дж/см 2от теплопроводности и 90 Дж⋅см –2от излучения, действительно получим 160 Дж/см 2, то есть несколько меньше значения Q 0 / S = 190 Дж/см 2. Напомним, что наши расчеты очень приблизительны: так, мы пренебрегли нагревом за счет конвекции, а также ролью начинки пиццы.

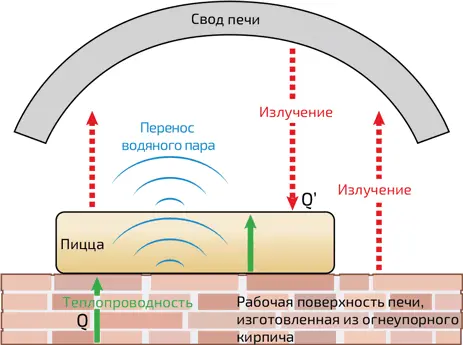
5. Процессы теплообмена при приготовлении пиццы. Излучение схематично обозначено красными стрелками, теплопроводность – зелеными, перенос водяного пара – голубыми дугами

Мощность теплового излучения с единицы площади при одной и той же температуре у разных источников различна, однако она всегда меньше или равна мощности, излучаемой абсолютно черным телом (см. главу 7, «От спектров атомов до спектра абсолютно черного тела»). Напомним, что так называют тело, которое поглощает все получаемое им излучение.

Мощность, которую такое тело излучает с единицы поверхности при температуре T , по закону, открытому физиком Йозефом Стефаном (1835–1893), равна σ T 4, где константа σ равна 5,67⋅10 –8Вт⋅м –2K –4. Когда Стефан в 1879 году представил на суд коллег этот закон, то его обоснование было чисто экспериментальным. И только в 1884 году австрийский физик Людвиг Больцман математически доказал, что мощность, излучаемая абсолютно черным телом, должна быть пропорциональна T 4. Это доказательство, основанное на общих принципах термодинамики, отличалось потрясающей элегантностью. И тем не менее сегодня оно представляет лишь исторический интерес. Дело в том, что формула, выведенная Планком в 1900 году (см. главу 7, «Формула Планка»), содержит гораздо больше информации, чем закон Стефана – Больцмана, поскольку она позволяет судить не только о полной излучаемой мощности абсолютно черным телом, а детализирует ее в зависимости от частоты. Таким образом, закон Стефана – Больцмана можно получить из формулы Планка путем простого интегрирования по частоте. И, таким образом, для эмпирической константы σ можно получить точное выражение в терминах фундаментальных физических постоянных: