Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Заметим, что работы де Бройля и Шрёдингера предшествовали открытию Гейзенбергом принципа неопределенности. Последний прост, краток, элегантен, однако содержит меньше информации, чем уравнение Шрёдингера.

Предложенная де Бройлем концепция связи между волнами и частицами, так называемый корпускулярно-волновой дуализм, привела к идее применения оптических методов исследования с заменой света на потоки частиц. Так, в 1927 году американские физики Клинтон Дэвиссон и Лестер Джермер бомбардировали электронами кристалл никеля. В результате они получили дифрактограммы, подобные возникающим при облучении кристаллов рентгеновскими лучами (см. врезку). Для интерпретации полученных дифракционных картин электронам следовало приписать определенную длину волны, и она совпадала с величиной, предсказанной де Бройлем. Таким образом, эксперимент блестяще подтвердил его гипотезу.

Принцип неопределенности позволяет получить интересную информацию о движении атомов в твердых телах. Под твердыми телами здесь мы будем подразумевать кристаллы (см. главу 9), поскольку при низких температурах кристаллическая структура является устойчивой формой существования почти всех чистых веществ. Атомы в кристалле не являются неподвижными: они колеблются вокруг положения равновесия. Амплитуда этих колебаний очень мала: расстояние между двумя соседними атомами всегда остается близким к своему среднему значению, которое составляет около нескольких десятых нанометра. Как правило, эти колебания обусловлены тепловым движением: чем температура выше, тем больше амплитуда колебаний (см. главу 22, врезку «Броуновское движение»). Что же происходит, когда температура опускается до абсолютного нуля (0 К, то есть –273,15 °C)? Можно предположить, что колебания прекращаются и атомы замирают. Однако в этом случае их положение было бы точно фиксировано, в то время как скорость была бы равна нулю, то есть Δ x = Δ p = 0, что нарушило бы соотношение неопределенности (1) (см. главу 22). Отсюда следует, что движение атомов прекратиться не может даже при абсолютном нуле температур: в этом случае тепловые колебания сменяются на «нулевые колебания».

Попробуем разобраться в этом подробнее на примере простого кристалла, состоящего из атомов лишь одного сорта (например, водорода, кислорода, железа). Упрощенное, но качественно приемлемое описание движения атома в кристалле относительно его соседей можно получить, предполагая, что при отклонении от положения равновесия на него действует возвращающая сила, пропорциональная расстоянию, так как если бы его удерживала пружина. В таком случае движение атома относительно положения равновесия описывается формулой x ( t ) = x 0 cos (ω t – α), где x 0 – максимальная амплитуда колебаний (для двух других координат формулы аналогичны). При этом скорость атома v x ( t ) = –ω x 0 sin (ω t – α). Соотношение неопределенности требует, чтобы Δ x Δ v ≥ ħ / m , и, следовательно, ω x 0 2было не менее ħ / m , где m – масса атома. Частота ω для большинства веществ лежит в диапазоне между 10 13и 10 14Гц (характерную частоту колебаний атома в твердых телах называют частотой Дебая). Заменяя массу m на A m n , где A – массовое число (см. главу 13, врезку «Элементы ядерной физики»), а m n – средняя масса нуклона (около 1,67⋅10 –27кг), получим, что x 0 в метрах должна составлять не менее 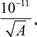Это условие устанавливает верхнюю границу для амплитуды нулевых колебаний в 1/100 нм, которая, как правило, мала в сравнении с равновесным расстоянием между соседними атомами. Поэтому нет оснований полагать, что нулевые колебания в твердых телах разрушают его устойчивость.

Сомнения могут оставаться только для наименьших значений A , то есть для водорода ( A = 1) и гелия ( A = 4). Оказывается, что только гелий (He) является исключением из правила: если давление не превышает 2,5 Мпа, то нулевые колебания действительно делают его кристаллическое состояние неустойчивым при любых температурах. Все остальные простые тела, включая водород H 2 , при приближении температуры к абсолютному нулю рано или поздно затвердевают при любом давлении.

Мы уже видели, что согласно квантовой механике ни в какой момент времени невозможно установить точные значения положения r →и скорости v →электрона, вращающегося вокруг ядра. Еще более необычными оказываются свойства его магнитного момента.

Магнитный момент – это векторная величина, характеризующая свойство определенных объектов ориентироваться в магнитном поле. Например, стрелка компаса располагается по магнитному полю Земли, указывая направление на Северный магнитный полюс. Многие из элементарных частиц и объектов атомного масштаба также обладают магнитным моментом: электрон, нейтрон, протон, а также бо́льшая часть ядер, атомов и ионов.

Пространственные составляющие магнитного момента обозначаются как µ x , µ y , µ z . Когда стрелка компаса сориентирована в определенном направлении, то четко определены и все три составляющие ее магнитного момента. В отличие от компаса, электрон или нейтрон являются объектами, принадлежащими к квантовому миру. Для них может быть измерена только одна из трех составляющих магнитного момента, при этом она способна принимать только два противоположных значения: –µ или +µ. Это, казалось бы, парадоксальное утверждение было подтверждено экспериментально: первыми опытные данные, говорящие в пользу квантования магнитного момента представителей квантового мира, еще в 1922 году получили Отто Штерн и Вальтер Герлах. В своих экспериментах они направляли пучок атомов серебра (которые благодаря электронам внешней оболочки обладают магнитным моментом) сквозь неоднородное магнитное поле. В результате было обнаружено, что этот пучок разделяется строго пополам, что и доказывает квантование магнитного момента всего на два дискретных значения (илл. 8). Действительно, если бы магнитный момент мог принимать хотя бы три значения, то и пучок делился бы натрое, а если бы магнитный момент атомов серебра мог меняться непрерывно, то и пучок просто расходился бы в конус.

Еще несколько слов о пучке атомов серебра. Выберем ось x вдоль направления магнитного поля. Тогда существует такое состояние атома серебра, в котором µ x = –µ, и другое, в котором µ x = +µ. Существует также состояние, при котором µ y = µ. Что произойдет, если частица находится в этом состоянии и измеряется компонент µ x ? Измерение с равной вероятностью даст µ x = –µ или µ x = +µ. Таким образом, среднее значение всех измерений µ x , которые можно произвести в состоянии µ y = µ, равно нулю. То же самое относится к среднему значению всех измерений µ x в состоянии µ y = –µ. Чтобы принять в расчет эти свойства, в квантовой механике считается, что состояние µ y = µ является «соединением» состояний µ x = –µ и µ x = µ.