Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

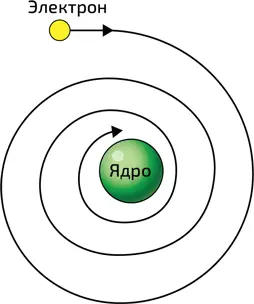
3. В классической физике атом Резерфорда был бы нестабилен: электрон в конце концов упал бы на ядро

В соответствии с этим принципом бедный электрон должен вращаться в области пространства некоторого размера с плохо определенной, но не равной нулю скоростью. И из этих смутных соображений мы собираемся оценить размер атома!

Пусть v и 2 R суть скорость электрона и диаметр сферы, в пределах которой он движется. Согласно формуле (1), 2 mRv > ħ . Следовательно, кинетическая энергия электрона, равная mv 2/2, не может быть меньше чем ħ 2/(8 mR 2). Добавляя электростатическую энергию его взаимодействия с протоном, находим неравенство для полной энергии электрона W :

где элементарный заряд e равен 1,6∙10 –19Кл, а ε o – диэлектрическая проницаемость вакуума, константа, равная 8,85∙10 –12Ф∙м –1.

Энергия W атома не может стать ниже минимума этого выражения, который, как легко понять, реализуется при R = R 0 , где

Равновесное состояние механической системы соответствует минимуму ее потенциальной энергии (см. главу 11, «Струны и резонатор»). Радиус атома R не может сильно превышать величину R 0 , потому что потенциальная энергия электрона при этом была бы слишком высока; но он не может быть и намного меньше R 0 , потому что тогда кинетическая энергия была бы слишком велика, а полная энергия должна сохраняться. Именно поэтому электрон и не падает на ядро! Выражение (3) дает нам представление о размере атома водорода – это примерно 1 ангстрем (десятая часть нанометра).

Пребывая в своем основном состоянии (минимума полной энергии), атом терять энергию не может. Однако он может ее получать, переходя при этом в то или иное «возбужденное» состояние. При этом бесконечно долго возбужденным он не остается – через некоторое время, излучая свет, атом возвращается в свое основное состояние. Этот свет соответствует излучению точно определенных частот, то есть спектр излучения атома является «линейчатым» (см. главу 7, «От спектров атомов до спектра абсолютно черного тела»). Частоты спектральных линий образуют так называемое дискретное множество, то есть их можно пронумеровать, например, в зависимости от интенсивности каждой из них. Чтобы объяснить происхождение такого линейчатого спектра, разумно предположить, что значения, которые может принимать энергия данного атома, также составляют дискретное множество. Поскольку свет может излучаться только в виде фотонов (см. главу 7, «От спектров атомов до спектра абсолютно черного тела»), то закон сохранения энергии требует, чтобы энергия hυ каждого фотона была равна разности между двумя допустимыми значениями энергии атома (илл. 4). Таким образом, дискретный вид спектра излучения объясняется, по крайней мере, качественно. Остается выяснить, почему значения энергии атома составляют дискретное множество.

В начале XX века вопрос о природе атома – мельчайшей частицы вещества, являющейся носителем его свойств, – был одним из центральных в физике. Предлагаемые модели, будучи внутренне противоречивыми или не соответствующими эксперименту, одна за другой опровергались. И вот в 1913 году датский физик Нильс Бор (илл. 2, справа) предложил математически простую теорию атома, объясняющую существующие экспериментальные данные, однако основанную на столь необычных допущениях, что он сам назвал их постулатами.

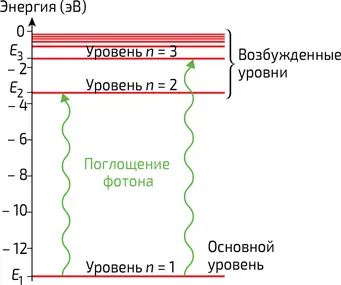
4. Энергетическая диаграмма атома водорода. Атом переходит из основного состояния в возбужденное путем поглощения фотона, энергия которого Δ E = hυ соответствует разнице между двумя энергетическими уровнями атома. Энергия выражается в электронвольтах (1 эВ = 1,6•10 –19Дж)

Нильс Бор, предлагая свою модель атома, ничего не знал о принципе неопределенности, до открытия которого оставалось еще 14 лет. В модели Бора, как и в модели Резерфорда, электрон вращается вокруг ядра, подобно тому как Земля вращается вокруг Солнца, однако при этом электрон может двигаться только по определенным орбитам (илл. 5). Например, круговые орбиты возможны только в том случае, когда произведение импульса mv электрона на радиус его орбиты R (это произведение называют «моментом импульса») является кратным постоянной Планка:

mvR = nħ. (4)

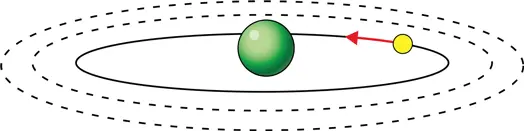
5. Атом водорода в представлении Резерфорда и Бора в начале XX века

Однако импульс электрона и радиус орбиты связаны также и тем обстоятельством, что действующая на электрон центробежная сила (см. главу 4, «Еще одна фиктивная сила: центробежная»), равная mv 2/ R , должна компенсировать силу электростатического притяжения. Для атома водорода, ядро которого состоит из протона, последняя равна – e 2/(4πε o R ). Отсюда уже можно найти радиусы R n–1 разрешенных орбит для каждого значения n . Так, для n = 1 находим уже знакомое нам значение R 0 , которое соответствует основному состоянию. Предоставим читателю самому вывести общую формулу, применимую к возбужденным состояниям электрона.

Модель Бора, разработанная в 1913 году, довольно хорошо описывала спектры излучения атомов (илл. 6), однако вскоре выявились и ее недостатки. Спустя десять лет теория Бора была концептуально расширена введением вероятностного описания нахождения электрона. Так оказалось, что значение R 0 (расстояние от электрона до ядра) в атоме водорода может считаться лишь некоей усредненной величиной; принцип неопределенности не позволяет четко определить расстояние между протоном и электроном.

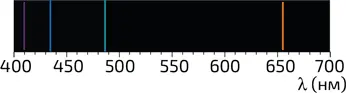
6. Модель Бора позволяет объяснить спектр излучения атома водорода в видимой области. Линии, расположенные вблизи длин волн излучения в 410, 434, 486 и 656 нм, соответствуют переходам на уровень, соответствующий n = 2 из возбужденных состояний n = 6, 5, 4 и 3 (см. илл. 4)