Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Отставим мороженицы в сторону и призовем на помощь технологию! Можно запросто получить отличное мороженое в течение нескольких десятков секунд, при условии наличия жидкого азота. В самом деле, переход азота из жидкого в газообразное состояние происходит при атмосферном давлении при температуре –196 °C. При заливке жидкого азота в заготовку (см. врезку выше) очень быстрое испарение азота (которое можно сопоставить с поведением воды, влитой в кипящее масло) провоцирует одновременно и мгновенное замораживание сливок в микрокристаллы, и образование пузырьков азота (илл. 4). Пузырьки, содержащиеся в таком мороженом, безвредны, ведь азот содержится и в воздухе, которым мы дышим, составляя более 78 % его объема.

4. Производство мороженого с использованием жидкого азота уже осуществляется в некоторых странах в специализированных кафе-мороженых. При контакте с жидким азотом водяной пар конденсируется, что служит причиной красивейшего явления: образования белоснежных облаков вокруг устройства…

В заключительной части, дорогой читатель, нам предстоит путешествие в удивительный, недоступный непосвященным мир. Мир, обычно открытый лишь тем, кого не пугают самые сложные уравнения и самые необычные математические методы.

Просим вас запастись терпением и довериться нам, как когда-то Данте доверился своему проводнику во время путешествия в Ад.

Не пытайтесь сразу разобраться во всем, потому что тайны квантового мира, как и закоулки Дантова Ада, бесчисленны и еще ждут своих исследователей. Скорее всего, некоторые из них до конца не поняты и вашими проводниками…

Нельзя точно измерить одновременно и положение, и скорость частицы. Этот «принцип неопределенности» противоречит здравому смыслу. Тем не менее он лежит в основе квантовой физики, которая описывает мир в масштабе нанометров.

1900 год, знаменующий начало XX века, является еще и датой возникновения квантовой механики. Именно тогда Макс Планк нашел решение задачи, поставленной Густавом Кирхгофом четырьмя десятилетиями ранее (см. главу 7, «Формула Планка»). Решение Планка основывалось на предположении, что энергия физической системы квантуется, то есть, например, если монохроматический свет частотой υ заключен в зеркальной камере, то его энергия обязательно окажется кратной одному «кванту» энергии, равному hυ, где h – постоянная Планка. Сперва эта гипотеза казалась относительно невинной. Однако спустя тридцать лет выяснилось, что она бросает вызов детерминистическому пониманию физики…

В 1927 году немецкий физик Вернер Гейзенберг сформулировал следующий принцип, называемый принципом неопределенности. Рассмотрим частицу массой m , которая движется по оси O x со скоростью v . Если нам удастся измерить ее скорость с точностью Δ v , то ее положение x оказывается невозможным определить с точностью Δ x более высокой, чем ħ /( m Δ v ), где ħ = 1,054⋅10 –34Дж⋅с [26] Предложенная Максом Планком постоянная h (см. главу 7, «Формула Планка») равна 2π ħ . Обычно именно h подразумевают под постоянной Планка. Далее постоянной Планка мы будем называть и h, и ħ . . Иными словами, m Δ x Δ v ≥ ħ . Это утверждение можно распространить и на движение частицы, перемещающейся в трехмерном пространстве. Вместо того чтобы рассуждать о ее скорости v →, часто вводят импульс p →= mv →. В этом случае соотношение неопределенности записывают следующим образом:

Δ x Δ p x ≥ ħ . (1)

Аналогично оно записывается и для двух других составляющих вектора импульса и координат.

Это неравенство удивительно. Законы Ньютона, о которых мы говорили в главе 4, врезке «Ньютоновская механика», позволяют, исходя из начальных условий, очень точно определить положение и скорость объекта в любой момент времени. В физике Ньютона, так называемой классической механике, нет места для неопределенности. Но этот детерминизм, свойственный макроскопическому миру, перестает действовать в атомном масштабе. Объясним, почему это происходит.

Для начала приведем иллюстрацию соотношений неопределенности. Направим поток частиц (например, электронов или нейтронов) на стенку, в которой есть отверстие диаметром Δ x (илл. 1). Некоторые из них пролетят через отверстие. В момент прохождения их положение определяется в плоскости стенки с точностью Δ x . При этом параллельные этой плоскости составляющие их скорости могут быть известны только с некоторой неопределенностью, обратно пропорциональной Δ x . Даже если скорость какой-то частицы при подлете строго перпендикулярна стенке, то после прохода через отверстие скорости всех прошедших частиц распределятся внутри некоторого телесного угла. Таким образом, здесь мы сталкиваемся с тем же явлением дифракции, что и в случае световых лучей, проходящих через узкую щель (см. главу 4, илл. 6).

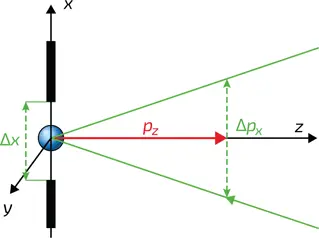
1. Если частица проходит через отверстие или щель ширины Δ x , то ее положение в направлении x известно с точностью Δ x . Согласно найденному Гейзенбергом неравенству, ее импульс в этом направлении может быть известен только с некоторой точностью Δ p x. Если частица является частью пучка, с импульсом p z вдоль оси O z , то прохождение пучка через щель вызывает его расхождение под углом, определяемым отношением Δ p x / p z

Согласно толкованию Гейзенберга (илл. 2, слева), квантовый индетерминизм является результатом взаимодействия наблюдаемой частицы с измерительным прибором. Вот как он рассуждал.

Предположим, мы хотим проанализировать движение электрона. Как это сделать? Невооруженный глаз, очевидно, не обладает достаточным разрешением, а что насчет микроскопа? Разрешение микроскопа определяется диапазоном длин волн λ наблюдаемого излучения. Для света они составляют порядка 100 нм (то есть 100 миллиардных частей метра), частицы меньшего размера не будут видны. Поэтому с помощью микроскопа невозможно увидеть атомы, размер которых составляет порядка 0,1 нм, и тем более – обнаружить электроны. Предположим, однако, что нам удалось сделать микроскоп с использованием электромагнитного излучения более короткой длины волны: рентгеновского или даже γ-излучения, длина волны которого составляет менее 0,01 нм (см. главу 3, «Цветовое зрение»). Стало бы такое изобретение идеальным инструментом для точного измерения положения и скорости электрона?