Анатолий Ахутин - История принципов физического эксперимента от античности до XVII века

В III части трактата Орем анализирует весьма интересные мысленно-экспериментальные ситуации. В гл. 2—4 он исследует некоторые особенности конфигураций в процессе их мысленного изменения. Он замечает, что при непрерывном изменении конфигурации дифформно-дифформные качества остаются таковыми на всем протяжении изменения, тогда как униформно-дифформные скачком, моментально преобразуются в дифформные (гл. 3). Мы убеждаемся здесь еще раз, насколько Орему важно только качество фигуры, «класс» ее конфигурации. Истолковывается же этот результат как некая абстрактная возможность.

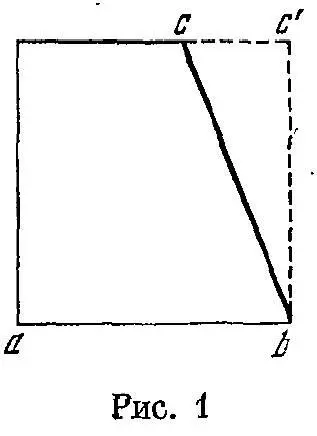
Далее Орем рассматривает аналогичную проблему перехода униформно-дифформного качества в абсолютно ( simpliciter )униформное в процессе непрерывного изменения угла наклона конфигурационного треугольника (гл. 4). В результате он приходит к выводу, что при непрерывном изменении угла в одной точке происходит скачкообразное изменение качества. «Отсюда,—пишет Орем,— следует, что при постепенном качественном изменении, при котором ничто не приобретается мгновенно ( subito ), возможно мгновенное изменение в какой-нибудь точке, линии или плоскости, до какой-либо суммарной широты или интенсивности» (III, 4, 702). Давая физическую интерпретацию этого теоретического вывода, Орем проводит следующий мысленный эксперимент (см. рис. 1). «...Пусть половина предмета аb — теплая в высшем градусе, а другая половина — униформно-дифформная, кончающаяся на высшем градусе в точке с и на неградусе в точке b. ...Вообразим теперь, что линия сb движется до тех пор, пока не займет положения перпендикулярного к ab , однако таким образом, что бы точка b все время оставалась неподвижной... В последнее мгновение, которое завершает качественное изменение, весь предмет имеет теплоту высшего градуса. Аналогично точка b имеет тогда теплоту высшего градуса, каковая точка непосредственно до того ( immediate ante ) была холодной в высшем градусе, т. е. не имела никакой теплоты». Следовательно, точка b мгновенно превращается из холодной в высшем градусе в теплую в высшем градусе. А это невозможно. «Отсюда,— говорит Орем,— может быть почерпнут аргумент в пользу того, что неделимая точка не есть что-либо реальное, ни линия, ни поверхность, хотя воображение их пригодно для лучшего постижения меры вещей...» Именно такое понимание математического будет характерно впоследствии для физиков XVII в. и, в частности, для Галилея. Однако Орем делает следующее заключение: «Можно было бы привести многое другое, придерживаясь указанного способа представления ( imaginatio ), но все это говорится не в физическом смысле и для некоторых кажется либо слишком трудным, либо невозможным» (111,4,702-703).

Наибольший интерес с точки зрения нашей темы представляет III часть трактата, озаглавленная «О приобретении и мере качества скорости» 111, в особенности главы, исследующие так называемую меру качеств (гл. 5—13).

Историки науки обращают здесь внимание главным образом на так называемое оремово правило, т. е. доказательство эквивалентности равноускоренного движения равномерному движению со средней скоростью 112 . Но Орем ставит вопрос гораздо шире. Здесь впервые речь идет о понятии, которое могло бы служить всеобщей мерой для точного сравнения различных качественных конфигураций. «Оремово правило» — только частный случай. Основным понятием, позволяющем ввести единую процедуру измерения, является понятие «количества качества» ( quantitas gualitatis ), которое соответствует понятию площади фигуры. «Итак,— говорит Орем,— чтобы найти меру качества или скорости и определить их отношения, нужно довериться геометрии и вернуться к геометрии». Ведь «мера или отношение двух любых линейных или поверхностных качеств, так же как и скоростей, соответствует мере и отношению фигур, посредством которых они в воображении сравниваются друг с другом» (III, 5, 703-704).

Это «сравнение фигур в воображении» получает теперь самостоятельную геометрическую разработку.

Понятие «количества качества» составляет тайну всего мысленно-экспериментирующего воображения Орема. Уже до всякого геометрического построения Орем замечает, что разная интенсивность действия не обязательно вызвана разным «объемом» наличного качества. Одно и то же качество, будучи по-разному распределено во времени или в пространстве, действует по-разному. Но только геометрическое представление позволяет ему ввести сюда известную определенность. Именно в таком контексте ставится Оремом вопрос об «эквивалентности» разных конфигураций. И именно поэтому он формулирует свое правило в самом общем виде: «Всякое качество, если оно униформно-дифформно, по своей величине таково, каким было бы униформное качество того же или равного ему предмета, соответствующее градусу средней точки того же предмета» (III, 7, 706).

Но наибольший интерес представляет дальнейшее развитие этой идеи. Орем замечает, что, поскольку у каждого линейного качества налично два «измерения»: экстенсивность и интенсивность, постольку любое конечное количество его, выражаемое конечной площадью определенной фигуры, может по своей интенсивности расти до бесконечности (без изменения количества), если в то же время происходит пропорциональное уменьшение экстенсивности, и обратно (III, 8, 708—709). Таким образом, возможная интенсивность качества, вообще говоря, не зависит от его общего количества. Этот, если можно так выразиться, «закон гиперболы» иллюстрируется далее не примере движения. Простой расчет показывает, что при гиперболическом росте моментальной скорости от некоторой конечной величины до бесконечности (речь, конечно идет о бесконечном ряде участков равномерного движения) суммарная скорость ( vilocitas totalis ) осталась бы величиной конечной.

Без сомнения, анализ этого взаимопревращения конечного и бесконечного является наивысшим достижением «конфигурационного» воображения, работа которого не осталась без последствий, хотя наиболее распространен был именно «калькуляторский» вариант.

Нам остается в заключение отметить основные вехи дальнейшей судьбы этого метода. Два немца, работавшие вместе с Оремом в Париже,— Альберт Саксонский и Марсилий Ингенский — усваивают и даже частично развивают его метод; в Италии Иоанн из Казале обнаруживает знакомство с методами «калькуляций», он вполне мог учиться непосредственно у Орема, который в 50-х годах XIV в. преподавал в Болонье.

Любопытно, что, как отмечает А. Майер, последующие сторонники учения о широте форм совершенно забывают метафизико-натурфилософский смысл его и обращают внимание только на его формальную сторону. Если бы не это, метод Орема вообще не сохранился до XVII в. и не был бы известен Галилею и Декарту. «А то, что он дошел до них, не подлежит никакому сомнению: для подтверждения своих расчетов как Галилей, так и Декарт с самого начала своей деятельности используют в качестве чего-то обычного и совершенно само собой разумеющегося те самые фигуры, которые в этой связи впервые использовал Орем» (с. 368—369).