Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]

Ожидаемая величина D 2 N для N > 1 может быть получена из D N − 1. Если после ( N − 1) шагов мы оказались на расстоянии D N − 1, то еще один шаг даст либо D N= D N − 1+ 1, либо D N= D N − 1− 1. Или для квадратов

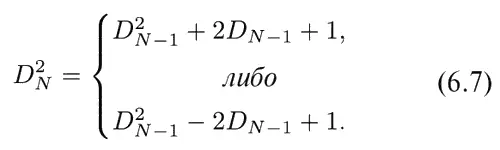
Если процесс повторяется большое число раз, то мы ожидаем, что каждая из этих возможностей осуществляется с вероятностью 1/ 2, так что средняя ожидаемая величина будет просто средним арифметическим этих значений, т. е. ожидаемая величина D 2 N будет просто D 2 N − 1+ 1. Но какова величина D 2 N − 1, вернее, какого значения ее мы ожидаем? Просто, по определению, ясно, что это должно быть «среднее ожидаемое значение» < D 2 N − 1>, так что

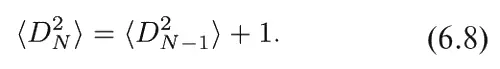
Если теперь вспомнить, что < D 2 1> = 1, то получается очень простой результат:

Отклонение от начального положения можно характеризовать величиной типа расстояния (а не квадрата расстояния); для этого нужно просто извлечь квадратный корень из D < 2 N > и получить так называемое среднее квадратичное расстояние D СК :

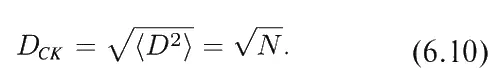
Мы уже говорили, что случайные блуждания очень похожи на опыт с подбрасыванием монет, с которого мы начали эту главу. Если представить себе, что каждое продвижение вперед или назад обусловливается выпадением «орла» или «решки», то D N будет просто равно N О − N Р, т. е. разности числа выпадений «орла» и «решки». Или поскольку N О + N Р = N (где N – полное число подбрасываний), то D N = 2 N О − N . Вспомните, что раньше мы уже получали выражение для ожидаемого распределения величины N О [она обозначалась тогда через k ; см. уравнение (6.5)]. Ну а поскольку N – просто постоянная, то теперь такое же распределение получилось и для D. (Выпадение каждого «орла» означает невыпадение «решки», поэтому в связи между N О и D появляется множитель 2.) Таким образом, на фиг. 6.2 график представляет одновременно и распределение расстояний, на которые мы можем уйти за 30 случайных шагов ( k = 15 соответствует D = 0, a k = 16 соответствует D = 2 и т. д.).

Отклонение N О от ожидаемой величины N /2 будет равно

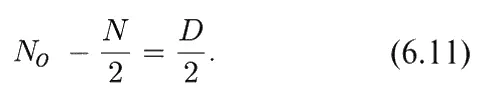
откуда для среднего квадратичного отклонения получаем

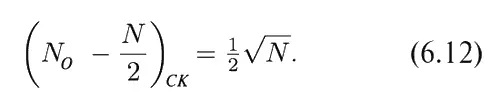
Вспомним теперь наш результат для D CK. Мы ожидаем, что среднее расстояние, пройденное за 30 шагов, должно быть равно √30 = 5,5, откуда среднее отклонение k от 15 должно быть 5,5: 2 ≈ 2,8. Заметьте, что средняя полуширина нашей кривой на фиг. 6.2 (т. е. полуширина «колокола» где-то посредине) как раз приблизительно равна 3, что согласуется с этим результатом.

Теперь мы способны рассмотреть вопрос, которого избегали до сих пор. Как узнать, «честна» ли наша монета? Сейчас мы можем, по крайней мере частично, ответить на него. Если монета «честная», то мы ожидаем, что в половине случаев выпадет «орел», т. е.

Одновременно ожидается, что действительное число выпадений «орла» должно отличаться от N /2 на величину порядка N /2, или, если говорить о доле отклонения, она равна

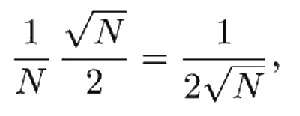
т. е. чем больше N , тем ближе к половине отношение N О / N.

На фиг. 6.6 отложены числа N О / N для тех подбрасываний монеты, о которых мы говорили раньше.

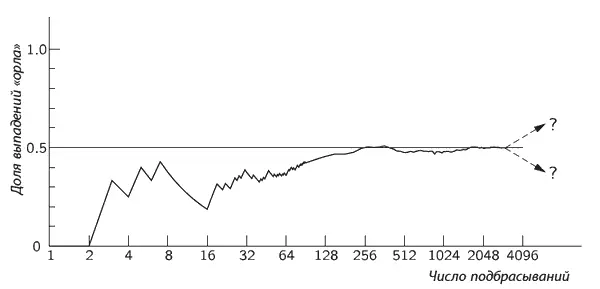
Фиг. 6.6. Доля выпадений «орла» в некоторой частной последовательности N подбрасываний монеты.

Как видите, при увеличении числа N кривая все ближе и ближе подходит к 0,5. Но, к сожалению, нет никаких гарантий , что для каждой данной серии или комбинации серий наблюдаемое отклонение будет близко к ожидаемому отклонению. Всегда есть конечная вероятность, что произойдет большая флуктуация – появление большого числа выпадений «орла» или «решки», – которая даст произвольно большое отклонение. Единственное, что можно сказать, – это если отклонения близки к ожидаемому 1/ 2√ N (скажем, со множителем 2 или 3), то нет оснований считать монету «поддельной» (или что партнер плутует).

Мы не рассматривали еще случаи, когда для монеты или какого-то другого объекта испытания, подобного монете (в том смысле, что возможны два или несколько достоверно не предсказуемых исхода наблюдения, например камень, который может упасть только на какую-то из двух сторон), имеется достаточно оснований полагать, что вероятности разных исходов не равны. Мы определили вероятность Р (O) как отношение < N О >/ N . Но что принять за величину < N О >? Каким образом можно узнать, что ожидается ? Во многих случаях самое лучшее, что можно сделать, это подсчитать число выпадений «орла» в большой серии испытаний и взять < N О > = N О (наблюденное). (Как можно ожидать чего-то еще?) При этом, однако, нужно понимать, что различные наблюдатели и различные серии испытаний могут дать другое значение Р (О), отличное от нашего. Следует ожидать , однако, что все эти различные ответы не будут расходиться больше чем на 1/ 2√ N [если Р (O) близко к половине], Физики-экспериментаторы обычно говорят, что «экспериментально найденная» вероятность имеет «ошибку», и записывают это в виде

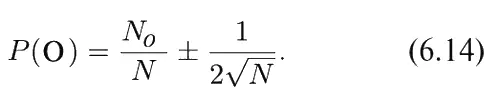
При такой записи подразумевается, что существует некая «истинная» вероятность, которую в принципе можно подсчитать , но что различные флуктуации приводят к ошибке при экспериментальном ее определении. Однако нет возможности сделать эти рассуждения логически согласованными. Лучше все-таки, чтобы вы поняли, что вероятность в каком-то смысле – вещь субъективная, что она всегда основывается на какой-то неопределенности наших познаний и величина ее колеблется при их изменении.