Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]

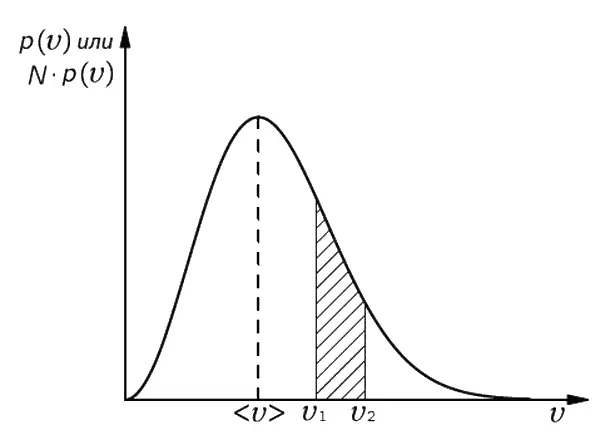
Фиг. 6.9. Распределение молекул газа по скоростям.

Скорость может иметь любую величину, однако больше шансов за то, что она окажется где-то в окрестности наиболее вероятного или ожидаемого значения < υ >.

О кривой, показанной на фиг. 6.9, часто говорят в несколько ином смысле. Если мы возьмем газ, заключенный в каком-то сосуде (скажем, объемом 1 л ), то окажется, что в нем имеется огромное количество молекул ( N ≈ 10 22). Поскольку p ( υ) Δ υ – вероятность того, что первая попавшаяся молекула будет лететь со скоростью, находящейся в интервале Δ υ , то, по определению, ожидаемое число молекул <���Δ N > со скоростью, находящейся в этом же интервале, будет равно

< ΔN > = N p (υ) Δυ. (6.21)

Поэтому Np ( υ ) можно назвать «распределением молекул по скоростям». Площадь под кривой между двумя значениями скоростей υ 1и υ 2[заштрихованная область на фиг. 6.9 для кривой Np ( υ )]представляет ожидаемое число молекул со скоростями между υ 1и υ 2. Но в газе, который содержит обычно огромное число молекул, отклонения от ожидаемого значения будут очень малы (порядка 1/√ N ), поэтому часто мы выбрасываем слово «ожидаемое» и говорим просто: «Число молекул со скоростями между υ 1и υ 2равно площади заштрихованного участка». Однако нужно все-таки помнить, что речь в таких случаях всегда идет о вероятном числе.

Понятия вероятности оказались очень полезны при описании поведения газа, состоящего из огромного количества молекул. Немыслимо же в самом деле пытаться определить положение и скорость каждой из 10 22молекул! Когда впервые теория вероятности была применена к таким явлениям, то это рассматривалось просто как удобный способ работы в столь сложной обстановке. Однако теперь мы полагаем, что вероятность существенно необходима для описания различных атомных процессов. Согласно квантовой механике, этой математической теории малых частичек, при определении положения частички и ее скорости всегда существует некоторая неопределенность. В лучшем случае мы можем только сказать, что существует какая-то вероятность того, что частица находится вблизи точки х.

Для описания местоположения частицы можно ввести плотность вероятности p 1( x ), так что p 1( x )Δ х будет вероятностью того, что частица находится где-то между х и х + Δ х . Если положение частицы установлено достаточно хорошо, то примерный вид функции p 1( x ) может иллюстрировать график, приведенный на фиг. 6.10, а. Точно такое же положение и со скоростью частицы: она тоже неизвестна нам точно. С некоторой вероятностью p ( υ) Δ υ частица может двигаться со скоростью, находящейся в интервале между υ и υ + Δ υ .

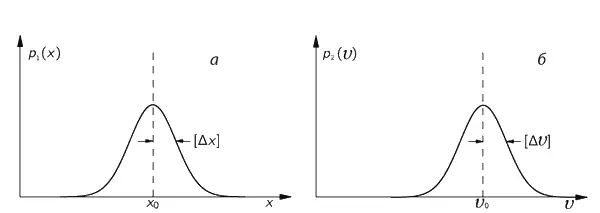
Фиг. 6.10. Плотности вероятности координаты (а) и скорости (б) частицы.

Один из основных результатов квантовой механики состоит в том, что эти две плотности p 1( x ) и p 2( υ ) не могут быть выбраны независимо в том смысле, что они обе не могут быть сколь угодно узкими. Если мы возьмем «полуширины» кривых p 1( x ) и p 2( υ ) и обозначим их соответственно [Δ х ] и [Δ υ ] (см. фиг. 6.10), то природа требует, чтобы произведение этих двух полуширин было не меньше величины h/m , где m – масса частицы, a h – некоторая фундаментальная физическая постоянная, называемая постоянной Планка . Это соотношение записывается следующим образом:

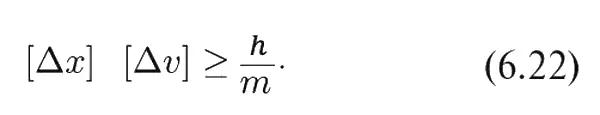
и называется принципом неопределенности Гейзенберга.

Чтобы это соотношение выполнялось, частица должна себя вести очень курьезно. Вы видите, что правая часть соотношения (6.22) постоянна, а это означает, что если мы попытаемся «приколоть» частицу в каком-то определенном месте, то эта попытка окончится тем, что мы не сможем угадать, куда она летит и с какой скоростью. Точно также если мы попытаемся заставить частицу двигаться очень медленно или с какой-то определенной скоростью, то она будет «расплываться» и мы не сможем точно указать, где она находится.

Принцип неопределенности выражает ту неясность, которая должна существовать при любой попытке описания природы. Наиболее точное и полное описание природы должно быть только вероятностным. Однако некоторым физикам такой способ описания приходится не по душе. Им кажется, что о реальном поведении частицы можно говорить только, когда одновременно заданы импульсы и координаты. В свое время на заре развития квантовой механики эта проблема очень сильно волновала Эйнштейна. Он часто качал головой и говорил: «Но ведь не гадает же Господь Бог „орел-решка“, чтобы решить, куда должен двигаться электрон!» Этот вопрос беспокоил его в течение очень долгого времени, и до конца своих дней он, по-видимому, так и не смог примириться с тем фактом, что вероятностное описание природы – это максимум того, на что мы пока способны. Есть физики, которые интуитивно чувствуют, что наш мир можно описать как-то по-другому, что можно исключить эти неопределенности в поведении частиц. Они продолжают работать над этой проблемой, но до сих пор ни один из них не добился сколько-нибудь существенного результата.

Эта присущая миру неопределенность в определении положения частицы является наиболее важной чертой описания структуры атомов. В атоме водорода, например, который состоит из одного протона, образующего ядро, и электрона, находящегося где-то вне его, неопределенность в местонахождении электрона такая же, как и размеры самого атома! Мы не можем поэтому с уверенностью сказать, где, в какой части атома находится наш электрон, и уж, конечно, не может быть и речи ни о каких «орбитах». С уверенностью можно говорить только о вероятности p ( r )Δ υ обнаружить электрон в элементе объема Δ υ на расстоянии r от протона. Квантовая механика позволяет в этом случае вычислять плотности вероятности p ( r ), которая для невозмущенного атома водорода равна Ae − r 2/ a 2.

Это – колоколообразная функция наподобие изображенной на фиг. 6.8, причем число а представляет собой характерную величину радиуса, после которого функция очень быстро убывает. Несмотря на то что существует вероятность (хотя и небольшая) обнаружить электрон на большем, чем а , расстоянии от ядра, мы называем эту величину «радиусом атома». Она равна приблизительно 10 −10 м.