Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]

Давайте вернемся к проблеме случайных блужданий, но теперь уже с некоторым изменением. Пусть в дополнение к случайному выбору направления шага (+ или −) некоторым непредсказуемым образом меняется также и его длина , причем требуется выполнение одного-единственного условия, чтобы длина шага в среднем была равна единице. Эта задача уже больше похожа на тепловое движение молекул в газе. Обозначим длину шага через S , которая, вообще говоря, может быть любой, но наиболее часто будет принимать значения где-то «вблизи» единицы. Для большей определенности давайте положим < S 2> = 1, или, что эквивалентно, S CK = 1. Вывод выражения для < D 2> при этом останется тем же, за исключением того, что уравнение (6.8) изменится теперь следующим образом:

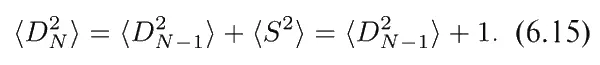
Так что, как и прежде,

Каково же в этом случае будет распределение расстояний! Какова, например, вероятность того, что после 30 шагов D окажется равным нулю? Вероятность этого равна нулю! Вообще вероятность любой заданной величины D равна нулю. Действительно, совершенно невероятно, чтобы сумма всех шагов назад (при произвольной длине каждого из них) в точности скомпенсировалась шагами вперед. В этом случае мы уже не можем построить график типа изображенного на фиг. 6.2.

Если же, однако, не требовать, чтобы D было в точности равно, скажем, нулю, или единице, или двум, а вместо этого говорить о вероятности получения D где-то вблизи нуля, или единицы, или двух, то при этом мы можем нарисовать график, подобный приведенному на фиг. 6.2. Назовем Р ( х, Δ x ) вероятностью того, что D будет находиться где-то внутри интервала Δ x в окрестности величины х (скажем, где-то между х и х + Δ x ). Если Δ x достаточно мало, то вероятность того, что D попадет в этот интервал, должна быть пропорциональна его ширине, т. е. Δ x . Поэтому мы можем утверждать, что

Р ( х , Δ х ) = р ( х ) Δ x. (6.17)

Функция р ( х ) называется плотностью вероятности.

Вид кривой р ( х ) зависит как от числа шагов N , так и от распределения шагов по длинам (т. е. от того, какую долю составляют шаги данной длины). К сожалению, я не могу здесь заниматься доказательством этого, а только скажу, что при достаточно большом числе шагов N плотность р ( х ) одинакова для всех разумных распределений шагов по длинам и зависит лишь от самого N. На фиг. 6.7 показаны три графика р ( х ) для различных N.

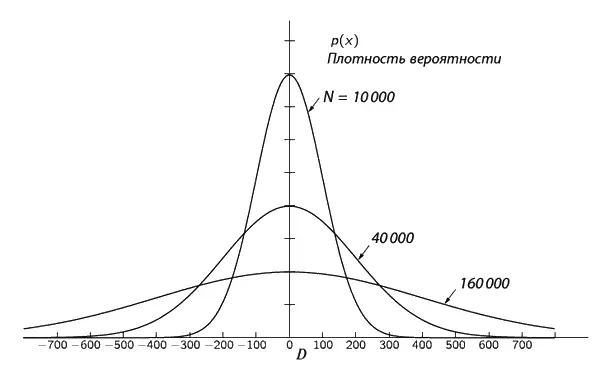
Фиг. 6.7. Плотность вероятности оказаться при случайном блуждании через N шагов на расстоянии D.

D измеряется в единицах средней квадратичной длины шага.

Заметьте, что «полуширины» этих кривых, как это и должно быть по нашим предыдущим расчетам, приблизительно равны √ N .

Вы, вероятно, заметили также, что величина р ( х ) вблизи нуля обратно пропорциональна √ N . Это происходит потому, что все кривые по форме очень похожи, только одни «размазаны» больше, а другие – меньше, и, кроме того, площади, ограниченные каждой кривой и осью х , должны быть равны. Действительно, ведь р ( х )Δ x ; это вероятность того, что D находится где-то внутри интервала Δ x (Δ x мало). Как определить вероятность того, что D находится где-то между x 1и x 2? Для этого разобьем интервал между x 1и x 2на узкие полоски шириной Δ x (фиг. 6.8) и вычислим сумму членов р ( х )Δ x для каждой такой полоски.

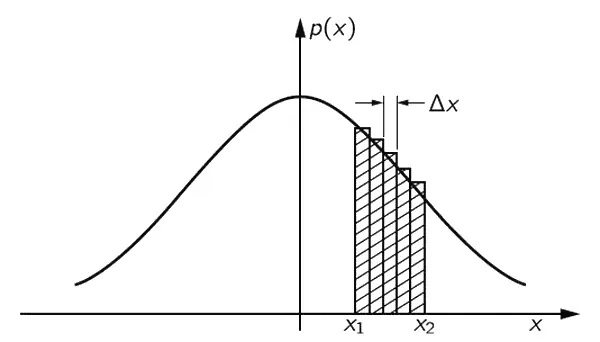
Фиг. 6.8. Вероятность [заштрихованная область под кривой р(х)] того, что при случайном блуждании пройденное расстояние D окажется между x 1и x 2.

Геометрически эта вероятность [запишем ее в виде P ( x 1< D < x 2)] равна площади заштрихованной области на фиг. 6.8. При этом чем ýже будут наши полоски, тем точнее результат. Поэтому можно записать

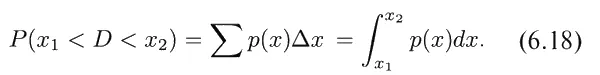
Площадь же ограничения всей кривой просто равна вероятности того, что D принимает какое-то значение между −∞ и +∞. Ясно, что она должна быть равна единице, т. е.

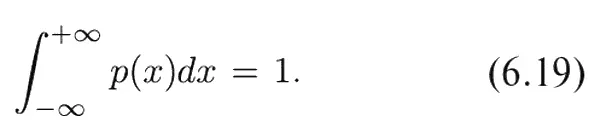
Ну а поскольку ширина кривых на фиг. 6.7 пропорциональна √ N , то, чтобы сохранить ту же площадь, их высота должна быть пропорциональна 1/√ N .

Плотность вероятности, которую мы только что описали, встречается наиболее часто. Она известна также под названием нормальной , или гауссовой , плотности вероятности и записывается в виде

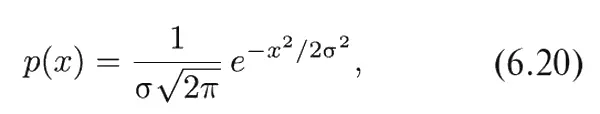
причем величина σ называется стандартным отклонением.

В нашем случае σ = √ N или √ N S CK, если средняя квадратичная длина шага отлична от единицы.

Мы уже говорили о том, что движения молекул или каких-то других частиц в газе похожи на случайные блуждания. Представьте себе, что мы открыли в комнате пузырек с духами или каким-то другим органическим веществом. Тотчас же молекулы его начнут испаряться в воздух. Если в комнате есть какие-то воздушные течения, скажем циркуляция воздуха, то они будут переносить с собой пары этого вещества. Но даже в совершенно спокойном воздухе молекулы будут распространяться, пока не проникнут во все уголки комнаты. Это можно определить по запаху или цвету. Если нам известен средний размер «шага» и число шагов в секунду, то можно подсчитать вероятность обнаружения одной или нескольких молекул вещества на некотором расстоянии от пузырька через какой-то промежуток времени. С течением времени число шагов возрастает и газ «расползается» по комнате, подобно нашим кривым на фиг. 6.7. Длина шагов и их частота, как вы узнаете впоследствии, связаны с температурой и давлением воздуха в комнате.

Вы знаете, что давление газа вызывается тем, что молекулы его бомбардируют стенки сосуда. Позднее, когда мы подойдем к количественному описанию этого явления, нам понадобится знать, с какой скоростью движутся молекулы, ударяясь о стенку, поскольку сила их ударов зависит от скорости. Однако говорить о какой-то определенной скорости молекул совершенно невозможно. В этом случае необходимо использовать вероятностное описание. Молекула может иметь любую скорость, но некоторые скорости предпочтительнее других. Все происходящее в газе можно описать, сказав, что вероятность того, что данная молекула движется с какой-то скоростью между υ и υ + Δ υ , будет равна p ( υ ) Δ υ , где p ( υ ) – плотность вероятности, которая зависит от скорости υ . Позднее я расскажу, как Максвелл, используя общие понятия и идеи теории вероятности, нашел математическое выражение для функции p ( υ ) [7] Максвелл получил выражение p ( υ ) = Cυ 2 e − aυ2 , где а – некоторая связанная с температурой постоянная, а С выбирается таким образом, чтобы полная вероятность была равна единице. . Примерный вид функции p ( υ )показан на фиг. 6.9.