Джирл Уокер - Новый физический фейерверк

Правила, по которым можно строить наклонную башню, определяют выбор нужной стратегии для получения максимального навеса. Допустим, они таковы, что вы не рассматриваете ограниченно устойчивые башни и должны либо просто ставить одну деталь на другую, либо укладывать ее только со сдвигом вправо. Тогда наиболее экономный метод строительства состоит в том, чтобы все детали, кроме верхних, просто ставить друг на друга — так, чтобы они образовали фундамент для «лестницы», идущей вправо. Например, чтобы получить навес в две длины детали (4 х ), вам понадобится минимум 11 деталей, из которых четыре верхних укладываются ступеньками (рис. 1.22в). Чтобы получить навес в nx , вам понадобится минимум 0,5 n ( n + 1) + 1 деталей, из которых n верхних образуют лестницу. (Для постройки ограниченно устойчивой башни можно убрать часть нижних деталей.)

Чтобы построить башню с заданным навесом и при этом использовать меньшее количество деталей, сначала укладывайте их со сдвигом влево, а потом вправо. Например, из 11 деталей можно построить устойчивую башню с навесом в 2,5 длины детали, то есть 5 х (рис. 1.22 г).

Знаменитая башня в итальянском городе Пиза начала крениться на южную сторону еще во время строительства, которое растянулось на два века. А когда наконец дело дошло до самой звонницы, ее поставили вертикально в надежде приостановить дальнейший наклон всей башни.

Пизанскую башню закрыли для туристов на многие годы после того, как упала башня в Падуе, убив при этом четырех человек. Но действительно ли знаменитая падающая башня была на волосок от падения? Максимальный угол ее наклона составил чуть более 5°, и хотя наклон с каждым годом увеличивался, этот прирост не превышал 0, 001° в год. Разве башня может упасть, если ее центр масс находится над основанием? А у Пизанской башни он бы вышел за его границы еще не скоро.

ОТВЕТ •Хотя наклон башни всегда был небольшим и проекция ее центра масс не покидала центральной части фундамента, перед недавно проводившимися реставрационными работами выяснилось, что наклон вызвал увеличение нагрузки на южную стену. Это увеличение привело к чудовищному давлению на нижние секции этой стены, а это угрожало тем, что стена могла выпятиться наружу и рухнуть. Опасность возрастала еще и из-за того, что спиральная лестница проходила по внешней стороне башни, а это уменьшало прочность всей конструкции. Наклон возник из-за рыхлости почвы под башней, и ситуация ухудшалась после каждого ливня. Чтобы стабилизировать башню и слегка уменьшить наклон, инженеры соорудили под башней дренажную систему для отвода воды и вынули грунт из-под северной части башни.

Как только первая костяшка домино из длинного ряда стоящих вертикально на одинаковом расстоянии друг от друга костяшек упадет на соседнюю, падения распространятся, как волна, по всему ряду. Сколько костяшек будет находиться в движении в каждый произвольный момент времени уже после того, как волна пошла, и чем определится скорость распространения этой волны? Расстояние между костяшками, естественно, не должно превышать длину каждой из них. А есть ли еще какой-то параметр, определяющий минимальное расстояние? Почему детские кубики не падают так же, как костяшки? Возникнет ли цепная реакция в ряду костяшек, если первая костяшка маленькая, а каждая следующая больше предыдущей в некоторое количество раз?

ОТВЕТ •Стоящая вертикально костяшка имеет два положения равновесия . Одно из них — когда костяшка стоит на меньшей грани вертикально (рис. 1.23а), а другое — когда она повернулась на небольшой угол относительно этого положения и ее центр масс находится как раз над ребром, на котором костяшка стоит (рис. 1.23б). В обоих положениях сила тяжести, которая, как мы предполагаем, приложена в центре масс костяшки, проецируется на основание костяшки. Однако про второе положение говорят, что в нем костяшка находится в положении неустойчивого равновесия . Действительно, любое малейшее воздействие выводит костяшку из этого положения, поскольку проекция силы тяжести сдвигается влево или вправо от ребра костяшки. Если она сдвигается вправо, как на рис. 1.23в, костяшка опрокинется.

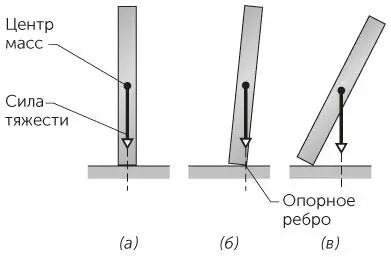
Рис. 1.23 / Задача 1.68.Костяшки домино проходят через положение неустойчивого равновесия.

Когда вы ударяете по первой костяшке в ряду, она пролетает через положение неустойчивого равновесия и падает плашмя на следующую. Если вы просто слегка подтолкнете первую костяшку, энергия от ее падения пойдет на выведение второй костяшки из равновесия. Если расстояние между костяшками мало, время падения на вторую костяшку и переданная ей энергия слишком малы, чтобы уронить и ее. Падение более вероятно при большем расстоянии — конечно, если оно не превышает длины костяшки. То же касается и остальных костяшек в ряду. (Конечно, вы могли бы как следует врезать по первой костяшке и не заботиться о соблюдении нужного расстояния между костяшками, но это будет неспортивно.)

В каждый произвольный момент времени в движении может участвовать пять или шесть костяшек. Волна набирает скорость по мере ее движения вдоль ряда костяшек, и эта скорость приближается к определенному значению, зависящему от расстояния между костяшками, трения между ними и того, как одна из них отскакивает от другой. Когда расстояние меньше, волна движется быстрее, и высота звука, издаваемого костяшками при падении, выше.

Профессор Лорн Вайтхед из Университета Британской Колумбии однажды описал, как цепная реакция распространяется по ряду костяшек домино, если все ребра каждой следующей костяшки в 1,5 раза больше, чем у предыдущей. Он опрокинул первую костяшку, «толкнув ее длинным тонким ватным жгутиком», а к моменту, когда опрокинулась тринадцатая костяшка, энергия в этой цепной реакции возросла в 2 миллиарда раз. Он посчитал, что в более длинном ряду таких же костяшек понадобилось бы только 32 штуки, чтобы снести «костяшку» размером с Эмпайр-стейт-билдинг. (Такого не сделал бы и Кинг-Конг.)

Когда падает высокая труба, вероятнее всего, она где-то треснет. Что вызывает появление разлома, где он возникает, и как труба согнется после того, как треснет (рис. 1.24а)? Вы можете проверить правильность ответа, опрокинув башенку из детских кубиков и проследив за тем, как эта башенка изогнется во время падения. А еще можно составить башенку из полых коротких цилиндров, которые удерживаются вместе эластичными нитками, пропущенными внутри, и опрокинуть ее.