Джирл Уокер - Новый физический фейерверк

ОТВЕТ •Когда мяч в гольфе отскакивает от стенки, это очень напоминает отражение светового луча от зеркала: и в том, и в этом случае угол падения равен углу отражения. Тогда представим, что мячик — это луч света, и ударим по мячу так, чтобы он полетел к бортику и отразился от него, как от зеркала. Из рис. 1.29 видно, как мяч нужно направить на стенку, чтобы он попал в лунку. Представьте себе, что стенка — это зеркало, в котором отражается лунка. Эта воображаемая лунка за бортиком находится на том же расстоянии от бортика, что и настоящая лунка. Если вы направите мяч в воображаемую лунку, он отразится от бортика и попадет в лунку реальную.

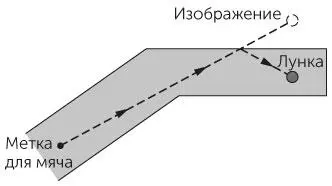
Рис. 1.29 / Задача 1.75.Вид сверху на трек для мини-гольфа с лункой.

Игроки, тренированные для гольфа (или бильярда, где практикуются такие же удары с отскоком), могут мысленно представить себе последовательность таких отскоков. Конечно, некоторые реальные обстоятельства, например шероховатость или наклон площадки или конкретные детали соударения с бортиком, могут помешать воплощению этого простого плана в жизнь, поэтому при игре в мини-гольф игрокам нужна и толика везения.

Если вы просто выпустите из руки мяч-попрыгунчик, он отскочит обратно и долетит почти до руки. А если вы бросите его вниз и даже закрутите его, куда он полетит?

Если вы закрутите мяч с нижним вращением, на себя ( бэкспин ), и бросите вниз под углом, он будет скакать между двумя точками на полу (рис. 1.30а). Если вместо этого вы придадите мячу верхнее вращение, вперед и вверх от себя ( топспин ), мячик начнет прыжками удаляться от вас, причем длинные прыжки будут чередоваться с короткими (1.30б). Может показаться, что высоты прыжков тоже чередуются, но это иллюзия. Если вы бросите мяч с нижним вращением под стол с тем, чтобы он отскочил от нижней поверхности столешницы и продолжил прыгать под столом, он может не захотеть оставаться под столом и полетит к вам (рис. 1.30в). Если вы бросите мяч на одну из параллельных вертикальных стен, расположенных близко одна к другой, мяч, вероятно, отскочит и полетит на вас (рис. 1.30 г). Что означает такое странное поведение и почему этот мячик-попрыгунчик настолько прыгучее обычного резинового мяча?

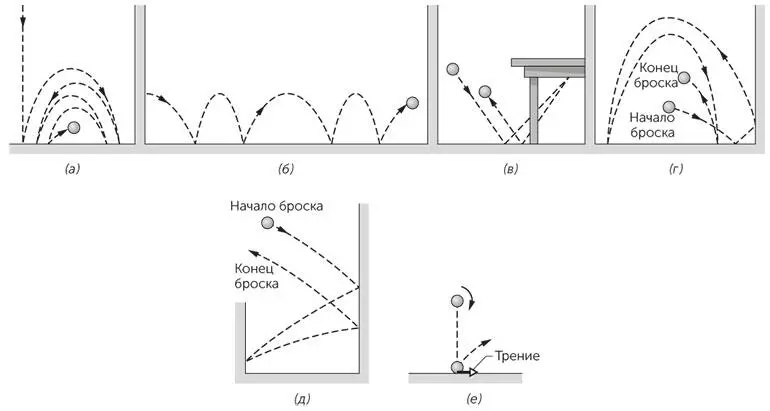
Рис. 1.30 / Задача 1.76.Фокусы с мячом-прыгуном при отскоках от одной или нескольких горизонтальных плоскостей (а) — (в), одной вертикальной стенки (г), двух вертикальных стенок (д). е) Трение закрученного мячика в момент соударения.

ОТВЕТ •Когда мячик закручен, его неровная поверхность мгновенно зацепляется за пол, и возникшее при этом трение посылает мяч в непредсказуемом направлении. Трение еще и изменяет вращение, так что следующий прыжок мяча может быть совсем не похож на предыдущий.

Например, если мяч брошен строго вниз с закруткой по часовой стрелке, если смотреть с одной стороны, трение будет направлено вправо (1.30д). Во время соударения мяч также испытает направленную вверх силу со стороны пола. Составляющая двух сил направит мяч вверх-вправо. А если вы бросите закрученный мяч вниз под углом, он может отскочить в сторону от вас, прямо вверх или назад на вас, в зависимости от направления и скорости закручивания, которые, в свою очередь, определят направление и величину силы трения.

Иллюзия того, что высоты отскоков чередуются, возникает из-за разницы в крутизне траекторий между отскоками. Когда прыжки меняются с длинного на короткий, угол отскока тоже меняется. (Эта иллюзия так сильна, что я дважды в своих книгах написал, что, видимо, высоты все-таки чередуются, хотя только что уверял, что они не могут отличаться.)

Мячики-попрыгунчики отскакивают так хорошо из-за того, что при отскоке в них возбуждаются необычные колебания. Когда простой резиновый мяч ударяется о пол, сжатие его нижней части вызывает колебания, период которых зависит от материала, из которого сделан мяч. Есть вероятность, что этот период отличается от времени, в течение которого длится соударение, и тогда мяч продолжит колебаться и после того, как он отскочил от пола. На колебания расходуется энергия, так что у мяча, летящего вверх, остается меньше энергии, и он не может подпрыгнуть очень высоко.

А в мячике-попрыгунчике есть ядро и оболочка, сделанная из другого материала. При такой конструкции колебания возбуждаются иначе, и время, в течение которого длится первое колебание, соответствует времени соударения мячика с полом. Точно в момент, когда нижняя поверхность мячика распрямляется и отталкивается от пола, колебание оболочки направлено наружу, от пола, а значит, оно помогает подкинуть мячик выше. В результате энергия колебаний вкладывается в движение вверх, и мяч подпрыгивает выше.

Чтобы определить направление, в котором отскочит закрученный мячик, нужно воспользоваться законами сохранения кинетической энергии и углового момента при отскоке. Вертикальная составляющая скорости просто меняет направление на противоположное. Горизонтальная составляющая в нижней точке тоже меняется на противоположную, но про нее что-то утверждать труднее, поскольку она зависит из горизонтальной скорости центра и скорости вращения мяча. Если вы векторно сложите вертикальную и горизонтальную скорости сразу после отскока, то сможете найти направление, в котором полетит отскочивший мяч.

В финале чемпионата мира 1975 года по хоккею на траве индийская команда выиграла из-за того, что рефери засчитал за гол бросок, в котором мяч пересек линию ворот, ударился в правую вертикальную стойку ворот (которая была за линией ворот) и отрикошетил обратно на игровое поле (рис. 1.31 — это вид сверху, рисунок выполнен не в масштабе). Хотя подобный отскок маловероятен и уж точно случается крайне редко в матчах, такое может произойти, если мяч летит под определенным углом по направлению к воротам и при этом вращается. Если удар нанесен вблизи левой стороны ворот, такой отскок произойдет при меньшей скорости вращения. Если угол подлета к воротам (угол между траекторией летящего мяча и линией ворот) превышает 25°, мяч обратно на поле отскочить не сможет. Никто не помнит точных деталей спора по поводу гола, но решение рефери звучало, по крайней мере, убедительно.

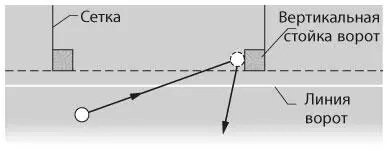
Рис. 1.31 / Задача 1.77.Вид сверху на поле для хоккея на траве и траекторию мяча, ударившегося о стойку ворот и отскочившего обратно на поле.