Ричард Фейнман - Том 1. Механика, излучение и теплота

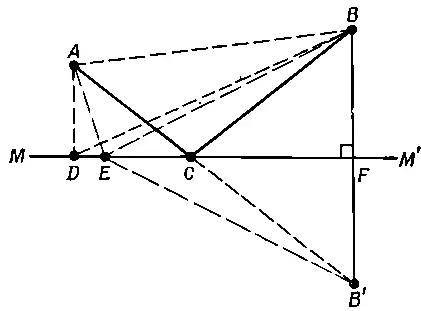
Фиг. 26.3. Иллюстрация принципа наименьшего времени.

Но если мы добавим дополнительное условие, что свет должен попасть на зеркало, отразиться от него и вернуться снова в точку В опять-таки за кратчайшее время, то ответить не так уж просто. Один путь — как можно скорее добраться до зеркала, а оттуда в точку B , т. е. по пути ADB . Путь DB , конечно, длинен. Если сдвинуться чуть-чуть вправо в точку Е , то первый отрезок пути немного увеличится, но зато сильно уменьшится второй, и время прохождения поэтому станет меньше. Как найти точку C , для которой время прохождения наименьшее? Воспользуемся для этого хитрым геометрическим приемом.

По другую сторону зеркала ММ ', на таком же расстоянии от него, что и точка B , построим искусственную точку B '. Затем проведем линию ЕВ '. Поскольку угол BFM прямой и BF = FB ', то ЕВ равно ЕВ '. Следовательно, сумма длин двух отрезков АЕ + ЕВ , пропорциональная времени их прохождения (если свет проходит с постоянной скоростью), равна сумме длин АЕ + ЕВ '. Теперь нужно выяснить, когда сумма длин будет наименьшей. Ответ : когда точка С будет лежать на прямой , соединяющей А и В '! Другими словами, нужно идти к мнимой точке В ' (мнимому изображению точки В ) и тогда мы найдем точку С . Далее, если АСВ '— прямая линия, угол BCF равен углу B ' CF и, следовательно, углу АСМ . Таким образом, утверждение о равенстве углов падения и отражения равносильно утверждению, что свет при отражении от зеркала в точку В выбирает путь, требующий наименьшего времени . Еще Герон Александрийский высказал утверждение, что свет при отражении идет из одной точки в другую по кратчайшему пути , так что идея принципа, как видите, не нова. Именно это вдохновило Ферма, и он попробовал применить этот принцип к явлению преломления. Но свет, преломляясь, очевидным образом идет не по кратчайшему пути , и тогда Ферма предложил другой принцип — свет выбирает путь, время прохождения по которому наименьшее .

Прежде чем перейти к вопросу о преломлении света, сделаем еще одно замечание об отражении от зеркала. Если поместить источник света в точку В и направить луч на зеркало, свет, отражаясь от зеркала, пройдет из В в А так, как будто бы источник находится в В ', а зеркала нет вообще . Наш глаз видит только тот свет, который действительно входит в него; и хотя источник расположен в точке В , зеркало направляет свет в глаз точно так, как будто источник находится в В ', и система глаза — мозг интерпретирует именно так это явление. Поэтому иллюзия, что источник или предмет находится за зеркалом, вызывается только тем фактом, что свет попадает в глаз физически именно так, как если бы предмет действительно был позади зеркала (если не принимать во внимание пыль на зеркале и то, что нам известно, что зеркало реально существует, и другие сведения, которые учитывает наш мозг).

Покажем теперь, что из принципа наименьшего времени вытекает закон Снелла для преломления. Мы должны, конечно, что-то предположить относительно скорости света в воде. Будем считать, что скорость света в воде меньше скорости света в воздухе, и отношение второй скорости к первой обозначим через n.

Наша задача по-прежнему состоит в том, чтобы на фиг. 26.4 попасть из точки А в В за наименьшее время .

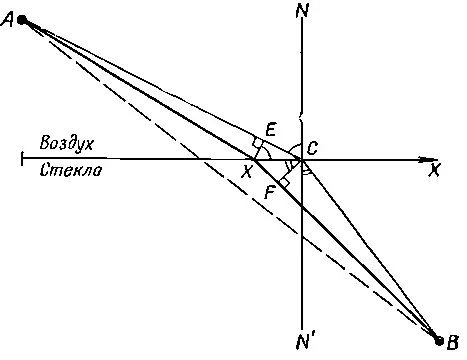
Фиг. 26.4. Иллюстрация принципа Ферма для случая преломления.

Чтобы убедиться, что путь по прямой здесь не самый быстрый, представим себе следующую ситуацию: хорошенькая девушка падает из лодки в воду в точке В и кричит, просит спасти. Линия X — это берег. Вы находитесь на суше в точке А и видите, что произошло, вы умеете плавать и умеете бегать. Но бегаете вы быстрее, чем плаваете. Что вам делать? Бежать по прямой к берегу? (Конечно!) Но, немного поразмыслив, вы поймете, что выгоднее пробежать несколько дольше по берегу, чтобы уменьшить ваш путь в воде, потому что в воде вы будете двигаться гораздо медленнее. (Рассуждая таким образом, лучше всего было бы заранее тщательно вычислить путь!) Во всяком случае, давайте попытаемся показать, что окончательное решение задачи — это путь АСВ , который занимает из всех возможных наименьшее время. Если этот путь кратчайший по времени, то любой другой окажется длиннее. Поэтому если отложить на графике зависимость времени от положения точки X, получится кривая, похожая на изображенную на фиг. 26.5, где точка С соответствует наименьшему времени.

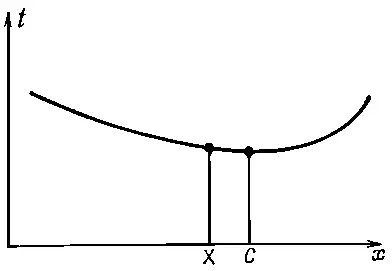
Фиг. 26.5 Наименьшее время получается при выборе точки С. Соседние точки приводят примерно к такому же времени прохождения.

Это означает, что для точек X вблизи С в первом приближении время прохождения практически одинаковое , так как в точке С наклон кривой равен нулю. Итак, наш способ найти искомый путь сводится к требованию, чтобы при небольшом изменении положения точки время прохождения не менялось. (Конечно, возникнут бесконечно малые изменения времени второго порядка, и они должны быть положительными при смещении в обе стороны от точки С .) Возьмем близкую точку X , вычислим время прохождения на пути АХВ и сравним его со старым путем АСB . Сделать это очень просто. Конечно, нужно еще, чтобы разность времен стремилась к нулю для малых расстояний ХС . Обратимся сначала к пути по суше. Если мы опустим перпендикуляр ЕХ , то легко увидим, что наш путь стал короче на длину ЕС . Можно сказать, что это расстояние мы выиграли. С другой стороны, опустив перпендикуляр CF , мы увидим, что в воде приходится проплыть дополнительное расстояние XF . В этом мы проиграли. С точки зрения экономии времени выигрывается время на отрезке ЕС , но теряется на отрезке XF . Эти два интервала времени должны быть равны, так как в первом приближении полное время прохождения не меняется. Предположив, что скорость в воде равна скорости в воздухе, умноженной на 1/n, получим

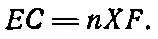(26.3)

Поэтому мы видим, что если нам удалось правильно выбрать точку С ( XC sin EXC = nXC sin XCF ) или мы сократили на длину общей гипотенузы ХС и заметили, что