Ричард Фейнман - Том 1. Механика, излучение и теплота
- Название:Том 1. Механика, излучение и теплота
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 1. Механика, излучение и теплота краткое содержание
Том 1. Механика, излучение и теплота - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
 (35.3)
(35.3)
Мы только что смогли подобрать два одинаковых желтых цвета; если оба цвета осветить розовым светом, то они останутся одинаковыми. Итак, добавив любой цвет к одинаковым цветам, получим одинаковый цвет. Обобщая все цветовые явления этого рода, можно сказать и по-другому: если цвета двух расположенных рядом друг с другом лучей света в одних условиях выглядят одинаковыми, то при любых смешениях они останутся одинаковыми и один луч может быть заменен другим при любом смешении цветов. Важным и интересным оказывается также то обстоятельство, что совпадение цветов не зависит от свойств зрения в момент наблюдения; известно, что если долго смотреть на яркую красную поверхность или яркий красный свет, а затем взглянуть на белый лист бумаги, то он покажется зеленоватым и другие цвета также будут восприниматься с искажениями (из-за того, что мы долго перед этим смотрели на ярко-красный цвет). Пусть мы добились совпадения двух желтых цветов, а затем долго смотрели на яркий красный цвет; повернувшись снова к желтым пятнам, мы обнаружим, что они уже не кажутся нам больше желтыми (какими именно они будут казаться — я не знаю, но только не желтыми). Однако в любом случае оба цвета по - прежнему будут казаться одинаковыми , т. е. способность глаза приравнивать два цвета сохраняется, несмотря на адаптацию глаза в условиях разной интенсивности. Очевидным исключением является только случай очень малой интенсивности, когда функция зрения переходит от колбочек к палочкам; здесь уже нельзя говорить о сравнении цветов, так как система зрения совсем другая.
Второй закон смешения цветов состоит в следующем: любой цвет может быть получен смешением трех разных цветов (в нашем случае зеленого, красного и синего). Мы уже продемонстрировали на двух примерах, что смешение трех цветов может дать самые разные цвета. Описанные выше законы, кроме того, очень интересны с математической точки зрения. Для тех, кого интересует математическая сторона проблемы, мы расскажем о ней более подробно. Возьмем три наших цвета — зеленый, красный и синий, обозначим их буквами А, В и С и назовем их основными . Тогда любой цвет может быть получен смешением определенных количеств каждого из данных трех цветов: например, цвет X создается смесью количества а цвета А , количества b цвета В и количества с цвета С :
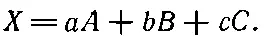 (35.4)
(35.4)
Составим теперь из тех же трех цветов новый цвет Y:
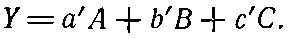 (35.5)
(35.5)
Тогда смесь цветов X и Y определяется суммами их компонент в основных цветах (как следствие двух главных законов цвета, приведенных выше):
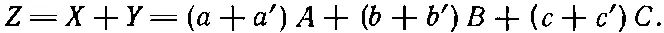 (35.6)
(35.6)
Это правило очень напоминает суммирование векторов, причем ( a, b, c ) играют роль компонент одного вектора, а ( a ', b ', c ') — компонент второго, и новый свет Z определяется «суммой» векторов. Такое соответствие постоянно привлекало к себе внимание физиков и математиков. В частности, Шредингер написал замечательную работу о цветовом зрении, в которой он развил теорию «векторного анализа» в применении к смеси цветов.
Возникает вопрос: как нужно выбрать основные цвета? В самом деле, никакого единственно правильного выбора нет. С практической точки зрения иногда оказывается более полезным выбирать определенные три цвета, потому что они дают в смеси большее число оттенков, но мы не будем сейчас на этом останавливаться.
Любые три по-разному окрашенных пучка света [25] Разумеется, за исключением того случая, когда один из трех цветов получается смешением двух других.
могут образовать какой угодно другой цвет , если их смешать в нужной пропорции.
Возможно ли показать на опыте действие этого удивительного, фантастического правила? Возьмем вместо красного, зеленого и синего света фонари с красным, синим, желтым фильтром и посмотрим, образует ли смесь этих цветов, скажем, зеленый цвет.
Смешивая эти три новых цвета в разных пропорциях, мы получаем целый спектр разных цветов. Но после целого ряда проб и ошибок мы убеждаемся, что ничего похожего на зеленый цвет получить не удается. А можем ли мы вообще образовать зеленый цвет? Да, можем. Но каким образом? Проектируя красный свет на зеленое пятно, мы можем затем подобрать точно такой же цвет путем смешения желтого и синего! Таким путем мы составляем две комбинации одного цвета, правда немного сжульничав, так как поместили красный в другую комбинацию. Но поскольку мы уже умеем разбираться в математических ухищрениях, то прекрасно понимаем, что вместо доказательства возможности составления цвета X из трех других цветов, например желтого, красного и голубого, мы установили, что красный плюс цвет X могут быть сделаны из желтого и голубого. Перенесем теперь красный цвет в другую часть равенства и будем интерпретировать его как отрицательную величину . Следовательно, в уравнениях типа (35.4) возможны как положительные, так и отрицательные значения коэффициентов, причем отрицательным величинам придается такой смысл, что их следует перенести в другую часть равенства со знаком плюс , тогда каждый цвет может быть действительно составлен из любых трех, и говорить о каком-то «правильном» выборе основных цветов бессмысленно.
Возникает вопрос, всегда ли при составлении смеси любого цвета входят три основных цвета с положительными коэффициентами? Нет, не всегда. Для каждой тройки основных цветов имеются цвета, для которых в смеси появляется отрицательный коэффициент, и поэтому однозначного способа выбора основной тройки не существует. В популярных книжках красный, зеленый и синий обычно называют основными цветами, но это объясняется только тем, что с их помощью можно создать более широкий набор цветов при положительных значениях коэффициентов в комбинации основных.
§ 4. Диаграмма цветности
Рассмотрим теперь смешивание цветов с математической точки зрения как некое геометрическое построение. Цвет, описываемый уравнением (35.4), можно представить вектором в трехмерном пространстве, где по трем осям отложены величины a, b и с, т. е. данному цвету соответствует точка в пространстве. Точка, соответствующая другому цвету, у которого компоненты равны а', b' и с', расположена в другом месте.
Читать дальшеИнтервал:
Закладка:




