Ричард Фейнман - Том 1. Механика, излучение и теплота

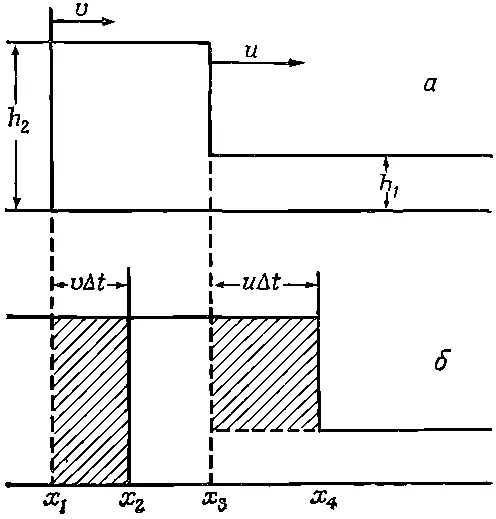
Фиг. 51.5. Два разреза высокого прилива в канале. Разрез б сделан на интервал времени Δt позднее разреза а.

Вообразите на минуту, что поверхность воды имеет такой вид, как изображено на фиг. 51.5,а, и что на верхнем уровне h 2она движется со скоростью v , а фронт со скоростью u надвигается на невозмущенную поверхность, высота которой h 1. Мы хотим определить скорость, с которой движется фронт. За промежуток времени Δ t вертикальная плоскость, проходившая вначале через точку x 1передвинется на расстояние v Δ t , т. е. от х 1до х 2, а фронт волны пройдет расстояние u Δ t .

Применим теперь законы сохранения вещества и импульса. Возьмем сначала первый из них: мы видим, что на единицу ширины канала количество вещества h 2 v Δ t , прошедшее мимо точки x 1(область, заштрихованная на фиг. 51.5,б), компенсируется другой заштрихованной областью, представляющей количество вещества (h 2- h 1) u Δ t . Разделив на Δ t , получим vh 2= u ( h 2- h 1). Но этого еще недостаточно, так как, хотя нам известны h 1и h 2, мы еще не знаем ни u , ни v , а хотим найти обе величины.

Следующим шагом будет использование закона сохранения импульса. Мы еще не касались вопросов давления в воде и прочей гидродинамики, но и так ясно, что давление в воде на какой-то глубине должно быть как раз достаточным, чтобы поддерживать столбик воды над этой глубиной. Следовательно, давление воды равно произведению плотности ρ на g и на глубину. Так как давление воды возрастает линейно с глубиной, то среднее давление на плоскость, проходящую, например, через точку х 1, равно 1/ 2ρ gh 2, что также представляет среднюю силу на единичную ширину и на единичную длину, толкающую плоскость к точке х 2. Чтобы получить полную силу, давящую на воду слева, мы должны еще раз умножить на h 2. С другой стороны, давление на рассматриваемую область справа дает противоположно направленную силу, которая по тем же причинам равна 1/ 2ρ gh 1 2. Теперь мы должны приравнять эти силы к скорости изменения импульса. Таким образом, нам нужно выяснить, насколько в случае, изображенном на фиг. 51.5,6, импульс больше, чем в случае, показанном на фиг. 51.5,а.

Мы видим, что дополнительная масса, которая приобрела скорость v равна просто ρh 2uΔt—ρh 2vΔt (на единицу ширины), а умножение ее на v дает дополнительный импульс, который должен быть приравнен к импульсу силы F Δ t :

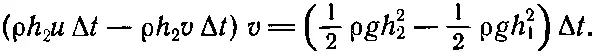
Исключая из этого уравнения v подстановкой vh 2= u ( h 2- h 1) и упрощая его, получаем окончательно u 2= gh 2( h 1+ h 2)/2 h 1.

Если разность высот очень мала, так что h 1и h 2приблизительно одинаковы, то скорость будет равна √( gh ). Как мы увидим позднее, это справедливо только при условии, что длина волны много больше глубины канала.

Аналогичную вещь можно сделать и для ударных волн, только теперь нужно добавить уравнение сохранения внутренней энергии, потому что ударная волна — явление необратимое. Действительно, если в задаче о высокой приливной волне проверить закон сохранения энергии, то мы увидим, что он не выполняется. Когда разность высот мала, то энергия почти сохраняется, но как только разность высот становится более заметной, возникают большие потери. Это проявляется в падении воды и водоворотах, показанных на фиг. 51.4.

С точки зрения адиабатического процесса в ударной волне тоже происходит аналогичная потеря энергии. Энергия в звуковой волне за ударным фронтом уходит на нагревание газа, что соответствует бурлению воды при высоком приливе. Оказывается, что необходимо решить три уравнения, чтобы описать все это для случая звука, причем нужно учесть, что температура за ударной волной и перед ней, как мы видели, не одинакова.

Если мы попытаемся пустить высокий прилив в обратную сторону (h 21), то окажется, что потеря энергии отрицательна. Но поскольку энергию взять неоткуда, высокий прилив не может поддерживать сам себя — он не стабилен. Если попытаться создать волну такого вида, то дальше она становится все более и более плоской, ведь зависимость скорости от высоты, которая раньше давала резкий фронт, в нашем случае будет работать в обратную сторону.

Следующий тип волн, о которых нам следует поговорить,— это волны в твердом теле. Мы уже рассмотрели звуковые волны в жидкости и газе, а между ними и звуковыми волнами в твердом теле имеется непосредственная аналогия. Если резко толкнуть твердое тело, то оно сожмется. Оно сопротивляется сжатию и в нем возникнут волны, аналогичные звуковым. Однако в твердом теле могут быть волны и другого рода, которых не бывает в жидкости. Если мы возбудим колебания твердого тела с помощью бокового давления (это называется сдвигом ), то тело стремится вернуться в начальное положение. Именно этим, по определению, твердое тело отличается от жидкого. Если искривить жидкость и подержать ее так немного, чтобы она успокоилась, а затем отпустить, то она останется в том же состоянии, но если мы возьмем твердое тело, похожее на дрожащий кусок желе, надавим на него и отпустим, то оно вернется назад, а в теле возникает волна сдвига , которая распространяется так же, как и волна сжатия. Во всех случаях скорость этих волн меньше скорости продольных волн. В каком-то отношении волны сдвига больше напоминают световые волны, ибо здесь мы тоже имеем дело с поляризацией. У звука нет никакой поляризации, это просто волна сжатия, а световые колебания имеют характерную ориентацию, перпендикулярную к направлению их распространения.

Итак, в твердом теле могут быть волны обоих сортов. Во-первых, там распространяются волны сжатия, аналогичные звуку в воздухе, и, во-вторых, волны сдвига. Если наше твердое тело не кристалл, то волна сдвига может быть поляризована в любом направлении. (Конечно, все твердые тела — кристаллы, но если мы возьмем кусок, состоящий из микрокристаллов всех ориентации, то кристаллическая анизотропия усредняется.)

Есть еще один интересный вопрос, касающийся звуковых волн. Что получится, если длина волны в твердом теле становится все меньше и меньше? До каких пор может это продолжаться? Ясно, что она не может стать меньше расстояния между атомами, ибо если под волной мы понимаем такое явление, когда одна точка идет вниз, а следующая — вверх и т. д., то кратчайшая возможная длина волны при этом, очевидно, равна межатомному расстоянию. Вам известно, что колебания могут быть как продольные, так и поперечные, длинноволновые и коротковолновые.