Ричард Фейнман - Том 1. Механика, излучение и теплота

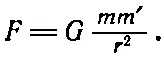
Если к этому добавить, что любое тело реагирует на приложенную к нему силу ускорением в направлении этой силы, по величине обратно пропорциональным массе тела, то способному математику этих сведений достаточно для вывода всех дальнейших следствий.

Но поскольку, как мы предполагаем, вы еще не столь талантливы, вооружим вас не только этими двумя аксиомами. Давайте вместе разберем следствия из них. Мы изложим вкратце историю открытия закона тяготения, остановимся на некоторых выводах из него и на его влиянии на историю, на загадках этого закона и на уточнении его Эйнштейном; мы хотим еще обсудить связь закона тяготения с другими законами физики. Всего этого в одну главу не уложишь, но в надлежащих местах других глав мы снова будем возвращаться к этому.

История начинается с древних; наши предки наблюдали движение планет среди звезд и в конце концов поняли, что планеты движутся вокруг Солнца — факт, заново открытый позже Коперником. Немного больше труда потребовалось, чтобы открыть, как именно они вращаются. В начале XV столетия шли большие дебаты о том, действительно ли планеты обращаются вокруг Солнца или нет. У Тихо Браге на этот счет было свое представление, далекое от того, что думали древние: мысль его состояла в том, что все споры о природе движения планет разрешатся, если достаточно точно измерить положение планет на небе. Если измерения точно установят, как движутся планеты, то не исключено, что из двух точек зрения удастся отобрать одну. Это была неслыханная идея — чтобы открыть что-то, лучше-де проделать тщательные опыты, чем приводить глубокие философские доказательства. Следуя ей, Тихо Браге многие годы изучал положения планет в своей обсерватории на острове Фюн, близ Копенгагена. Он составил объемистые таблицы, впоследствии, после смерти Тихо, изученные математиком Кеплером. Из его данных Кеплер и извлек замечательные, очень красивые и простые законы, управляющие движением планет.

Прежде всего Кеплер понял, что все планеты движутся вокруг Солнца по кривой, называемой эллипсом , причем Солнце находится в фокусе эллипса. Эллипс — это не совсем овал, это особым образом точно определяемая кривая. Получить такую кривую можно, воткнув в фокусы по булавке, к которым привязана нить, натянутая карандашом. Выражаясь математически, это — геометрическое место точек, сумма расстояний которых от двух заданных точек (фокусов) постоянна. Или, если угодно, это — окружность, видимая под углом к своей плоскости (фиг. 7.1).

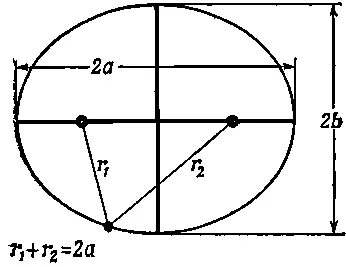
Фиг. 7.1 .Эллипс.

Другое наблюдение Кеплера состояло в том, что планеты движутся не с постоянной скоростью: поблизости от Солнца — быстрее, а удаляясь — медленнее. Более точно: пусть планета наблюдается в два последовательных момента времени, скажем на протяжении недели, и к каждому положению планеты проведен радиус-вектор [9] Отрезок, соединяющий Солнце с точкой орбиты. . Дуга орбиты, пройденная планетой за неделю, и два радиус-вектора ограничивают некоторую площадь, заштрихованную на фиг. 7.2.

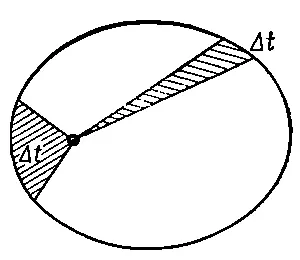
Фиг. 7.2. Кеплеров закон площадей.

Если такие же наблюдения в течение недели проделать в другое время, когда планета движется по дальнему участку орбиты (т. е. медленнее), то построенная таким же способом фигура окажется по площади равной прежней. Итак, в соответствии со вторым законом орбитальная скорость любой планеты такова, что радиус «заметает» равные площади в равные интервалы времени.

Третий закон был открыт Кеплером гораздо позже; он другого рода, нежели первые два: он уже касается не одной планеты, а связывает между собой разные планеты. Закон утверждает, что если сравнить между собой период обращения и размеры орбиты двух планет, то периоды пропорциональны полуторной степени размеров орбит. Здесь период — это время, нужное планете для того, чтобы обойти всю орбиту; размер же измеряется длиной наибольшего диаметра эллиптической орбиты, ее большой оси. Считая орбиты кругами (чем они почти и являются), можно сказать проще: время одного оборота по кругу пропорционально его диаметру (или радиусу) в степени 3/2. Итак, три закона Кеплера таковы:

1. Все планеты движутся вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

2. Радиус-вектор от Солнца до планеты «заметает» равные площади в равные интервалы времени.

3. Квадраты времен обращения двух планет пропорциональны кубам больших полуосей их орбит: Т 2~ а 3.

В то время, когда Кеплер открывал эти законы, Галилей изучал законы движения. Он пытался выяснить, что заставляет планеты двигаться. (В те дни одна из предлагавшихся теорий утверждала: планеты движутся потому, что за ними летят невидимые ангелы, которые взмахами своих крыльев гонят планеты вперед. Ныне эта теория, как вы вскоре увидите, несколько видоизменена! По-видимому, чтобы заставить планеты вращаться, невидимые ангелы обязаны витать во всевозможных направлениях и обходиться без крыльев. В остальном эти теории схожи!) И Галилей открыл одно знаменательное свойство движения, достаточное, чтобы понять эти законы. Это — принцип инерции : если при движении тела его ничто не касается, ничто не возмущает, то оно может лететь вечно с постоянной скоростью и по прямой. (А почему это так? Мы этого не знаем, но так уж оно повелось.)

Ньютон затем видоизменил эту мысль, говоря, что единственный способ изменить движение тела — это применить силу . Если тело разгоняется, значит сила была приложена в направлении движения . Если тело повернуло в сторону , то сила была приложена сбоку . Если, например, привязать камень к бечевке и вертеть им по кругу, то, чтобы удержать его на окружности, нужна сила. Мы должны все время натягивать бечевку. Закон состоит в следующем: ускорение, производимое силой, обратно пропорционально массе . Или иначе: сила пропорциональна массе и ускорению . Чем массивнее тело, тем большая сила необходима, чтобы создать нужное ускорение. (Массу можно измерить, привязав к веревке другой камень и вертя им по тому же кругу с той же скоростью. Так можно обнаружить, что массивным телам нужна большая сила.) Из этих рассуждений последовала блестящая мысль: чтобы удержать планету на ее орбите, никакой касательной силы не нужно (ангелам нет нужды летать по касательной), потому что планета и так будет лететь в нужном направлении. Если бы ничего ей не мешало, она бы удалилась по прямой линии . Но истинное движение уклоняется от этой прямой и отклоняется как раз поперек движения, а не по движению. Иными словами, благодаря принципу инерции сила, потребная для управления движением планет вокруг Солнца, это не сила, вращающая их вокруг Солнца, а сила, направленная к Солнцу (ну, а раз сила направлена к Солнцу, то, бесспорно, это и есть тот самый ангел!).