Ричард Фейнман - Том 2. Электромагнетизм и материя

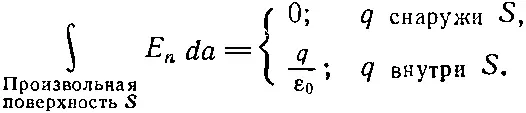(4.32)

Давайте вернемся к нашей аналогии с «дробинками» и посмотрим, есть ли в ней смысл. Наша теорема утверждает, что суммарный поток дробинок через поверхность равен нулю, если поверхность не окружает собой ружье, стреляющее дробью. А если ружье окружено поверхностью, то какого бы размера или формы она ни была, количество проходящих через нее дробинок всегда одно и то же — оно дается скоростью, с которой дробинки вылетают из ружья. Все это выглядит вполне разумно для сохраняющихся дробинок. Но сообщает ли эта модель нам хоть что-то сверх того, что получается просто из уравнения (4.32)? Никому не удалось добиться того, чтобы «дробинки» произвели на свет что-нибудь сверх этого закона. Кроме него, они порождают только ошибки. Поэтому-то мы сегодня предпочитаем чисто абстрактное представление об электромагнитном поле.

Наш изящный результат — уравнение (4.32) — был доказан для отдельного точечного заряда. А теперь допустим, что имеются два заряда: заряд q 1—в одной точке и заряд (q 2— в другой. Задача выглядит уже потруднее. Теперь электрическое поле, нормальную составляющую которого мы интегрируем, это уже поле, созданное обоими зарядами. Иначе говоря, если E 1—то электрическое поле, которое создал бы один только заряд q 1,a E 2— электрическое поле, создаваемое одним зарядом q 2, то суммарное электрическое поле равно Е= Е 1+ Е 2. Поток через произвольную замкнутую поверхность S равен

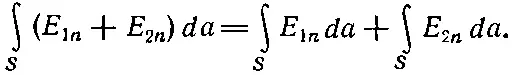(4.33)

Поток при наличии двух зарядов — это поток, вызванный одним зарядом, плюс поток, вызванный другим. Если оба находятся снаружи S , то поток сквозь S равен нулю. Если q 1находится внутри S , а q 2— снаружи, то первый интеграл даст q 1/ε 0, а второй — нуль. Если поверхность окружает оба заряда, то каждый внесет вклад в интеграл и поток окажется равным (q 1+q 2)/ε 0. Общее правило очевидно: суммарный поток из замкнутой поверхности равен суммарному заряду внутри нее, деленному на ε 0.

Этот результат представляет собой важный общий закон электростатического поля, и называется он теоремой Гаусса, или законом Гаусса:

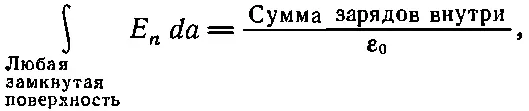(4.34)

или

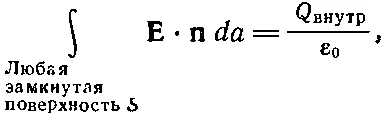(4.35)

где

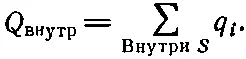(4.36)

Если мы описываем расположение зарядов на языке плотности зарядов ρ, то мы можем считать, что каждый бесконечно малый объем dV содержит «точечный» заряд ρ dV . Тогда сумма по всем зарядам есть интеграл

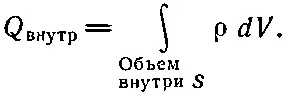(4.37)

Из нашего вывода видно, что закон Гаусса вытекает из того факта, что показатель степени в законе Кулона в точности равен двум. Поле с законом 1/r 3, да и любое поле 1/r nс n≠2, не привело бы к закону Гаусса. Значит, закон Гаусса как раз выражает (только в другой форме) закон сил Кулона, действующих между двумя зарядами. Действительно, отправляясь от закона Гаусса, можно вывести закон Кулона. Оба они совершенно равноценны до того момента, пока силы между зарядами действуют радиально.

Теперь мы хотим записать закон Гаусса на языке производных. Чтобы это сделать, применим его к поверхности бесконечно малого куба. В гл. 3 мы показали, что поток Еиз такого куба равен дивергенции ∇· Е, помноженной на объем dV куба. Заряд внутри dV по определению ρ равен ρ dV , так что закон Гаусса дает

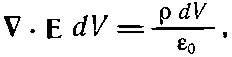
или

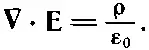(4.38)

Дифференциальная форма закона Гаусса — это первое из наших фундаментальных уравнений поля в электростатике, уравнение (4.5). Мы теперь показали, что два уравнения электростатики (4.5) и (4.6) эквивалентны закону силы Кулона. Разберем один пример применения закона Гаусса (другие примеры будут рассмотрены позже).

Одной из самых трудных задач, которую пришлось нам решать, когда мы изучали теорию гравитационного притяжения, было доказать, что сила, создаваемая твердым шаром на его поверхности, такая же, как если бы все вещество шара было сконцентрировано в его центре. Много лет Ньютон не решался обнародовать свою теорию тяготения, так как не был уверен в правильности этой теоремы. Мы доказали ее в вып. 1, гл. 13, взяв интеграл для потенциала и вычислив силу тяготения по градиенту. Теперь эту теорему мы можем доказать очень просто. Но на этот раз мы докажем не совсем ее, а сходную теорему для однородно заряженного электричеством шара. (Поскольку законы электростатики и тяготения совпадают, то то же доказательство может быть проведено и для поля тяготения.)

Зададим вопрос: каково электрическое поле Ев точке Р где-то снаружи сферы, наполненной однородно распределенным зарядом? Так как здесь нет «выделенного» направления, то законно допустить, что Евсюду направлено прямо от центра сферы. Рассмотрим воображаемую сферическую поверхность, концентрическую со сферой зарядов и проходящую через точку Р (фиг. 4.11).

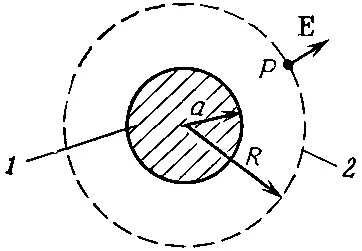
Фиг. 4.11. Применение закона Гаусса для определения поля однородно заряженного шара. 1 — распределение заряда ρ; 2 — гауссова поверхность S.

Для этой сферы поток наружу равен

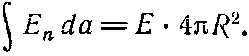
Закон Гаусса утверждает, что этот поток равен суммарному заряду сферы Q (деленному на ε 0):

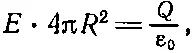
или

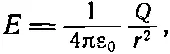(4.39)

а это как раз та формула, которая получилась бы для точечного заряда Q . Мы решили проблему Ньютона проще, без интеграла. Конечно, это кажущаяся простота; вам пришлось затратить какое-то время на то, чтобы разобраться в законе Гаусса, и вы можете думать, что на самом деле время нисколько не сэкономлено. Но когда вам придется часто применять эту теорему, то она практически окупится. Все дело в привычке.