Ричард Фейнман - Том 2. Электромагнетизм и материя

В некоторых молекулах из-за самой их формы заряды несколько разделены даже в отсутствие внешних полей. В молекуле воды, например, имеется отрицательный заряд на атоме кислорода и положительный заряд на обоих атомах водорода, которые расположены несимметрично (фиг. 6.2).

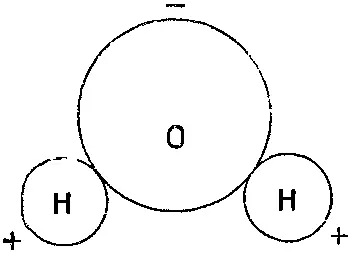
Фиг. 6.2. Молекула воды Н 2 O.

Хоть заряд всей молекулы равен нулю, все же имеется распределение заряда с небольшим преобладанием отрицательного заряда на одной стороне и положительного на другой. Это расположение, конечно, не такое простое, как у двух точечных зарядов, но если смотреть на него издалека, оно действует как диполь. Как мы увидим чуть позже, поле на больших расстояниях нечувствительно к мелким деталям расположения.

Взглянем теперь на поле двух зарядов противоположных знаков, расстояние d между которыми мало. Если d станет нулем, два заряда сойдутся в одном месте, два потенциала сократятся, поле исчезнет. Но если они не совсем слились, то можно получить хорошее приближение к потенциалу, разложив слагаемые в (6.8) в ряд по степеням малой величины d (по формуле бинома Ньютона). Оставляя только первые степени d , мы напишем

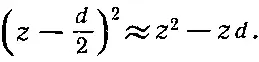
Удобно обозначить

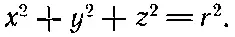
Тогда

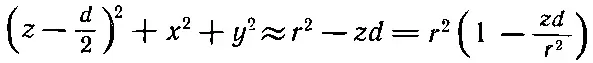
и

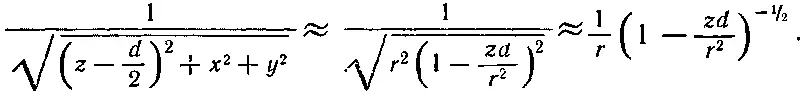
Разлагая в биномиальный ряд [1-(zd/r 2)] -1/2и отбрасывая члены с высшими степенями d , мы получаем

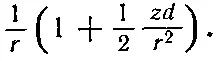
Подобно этому, и

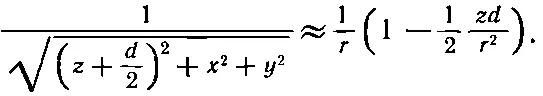
Вычитая эти два члена, имеем для потенциала

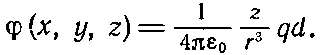(6.9)

Потенциал, а значит, и поле, являющееся его производной, пропорциональны qd — произведению заряда на расстояния между зарядами. Это произведение называется дипольным моментом пары зарядов, и мы обозначим его символом р ( не путайте с импульсом!):

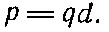(6.10)

Уравнение (6.9) можно также записать в виде

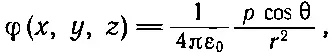(6.11)

так как z/r=cosθ, где θ — угол между осью диполя и радиус-вектором к точке ( х, у, z ) (см. фиг. 6.1). Потенциал диполя убывает как 1/r 2при фиксированном направлении (а у точечного заряда он убывает как 1/ r ). Электрическое поле Едиполя поэтому убывает как 1/r 3.

Мы можем записать нашу формулу и в векторном виде, если определим р , как вектор, абсолютная величина которого равна р , а направление выбрано вдоль оси диполя от q -к q +. Тогда

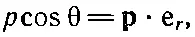(6.12)

где е r— единичный радиальный вектор (фиг. 6.3).

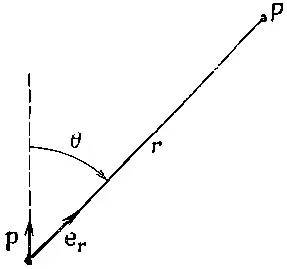
Фиг. 6.3. Векторные обозначения, для диполя.

Кроме того, точку (x, y, z) можно обозначить буквой r. Итак,

Дипольный потенциал :

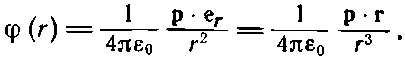(6.13)

Эта формула справедлива для диполя произвольной ориентации и положения, если r— вектор, направленный от диполя к интересующей нас точке.

Если нас интересует электрическое поле диполя, то нужно взять градиент φ. Например, z-компонента поля есть -∂φ/∂ z . Для диполя, ориентированного вдоль оси z , мы можем использовать (6.9):

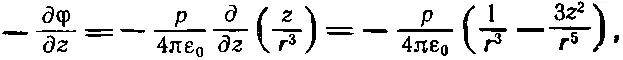
или

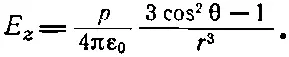(6.14)

А х - и y -компоненты равны

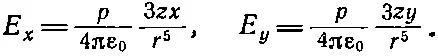
Из этих двух компонент можно составить компоненту, перпендикулярную к оси z, которая называется поперечной компонентой E ┴:

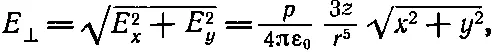
или

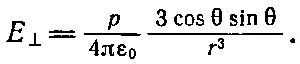(6.15)

Поперечная компонента Е ┴лежит в плоскости ху и направлена прямо от оси диполя. Полное поле, конечно, равно

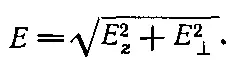
Поле диполя меняется обратно пропорционально кубу расстояния от диполя. На оси при θ=0 оно вдвое сильнее, чем при θ=90°. При обоих этих углах электрическое поле обладает только z-компонентой. Знаки ее при я=0 и при z=90° противоположны (фиг. 6.4).

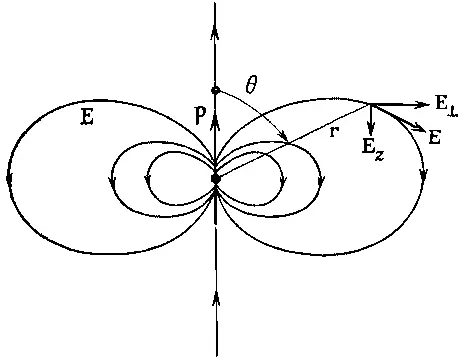
Фиг. 6.4. Электрическое поле диполя.

Здесь, пожалуй, уместно сделать общее замечание, касающееся векторного анализа. Хотя его теоремы и доказаны в общем виде, однако, приступая к расчетам и анализу какой-либо задачи, следует с толком выбирать направление осей координат. Вспомните, что когда мы вычисляли потенциал диполя, то ось выбиралась не как попало, а мы направили ее по оси диполя. Это намного облегчило нашу задачу. Потом уже уравнения были переписаны в векторной форме и сразу перестали зависеть от выбора системы координат. Теперь стало возможным выбирать какую угодно систему координат, зная, что формула отныне всегда будет справедлива. Вообще нет смысла вводить произвольную систему координат, где оси направлены под каким-то сложным углом, если можно в данной задаче выбрать систему получше, а уже в самом конце выразить результат в виде векторного уравнения. Так что старайтесь использовать то преимущество векторных уравнений, что они не зависят ни от какой системы координат.