Ричард Фейнман - Том 3. Квантовая механика

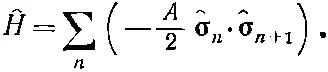(13.2)

В этом уравнении для удобства написан множитель А /2 (так что некоторые из дальнейших уравнений в точности совпадут с уравнениями из гл. 11).

Каково же наинизшее состояние системы? Состояние наинизшей энергии это то состояние, когда все спины параллельны, скажем все глядят вверх [49] Основное состояние здесь на самом деле «вырождено». Существуют и другие состояния с той же энергией, например, когда все спины смотрят вниз или в любую другую сторону. Но наложение самого слабого внешнего поля в направлении z снабдит все эти состояния различной энергией, и истинным основным состоянием окажется как раз то, которое мы выбрали. . Это состояние можно обозначить |... + + + + ...>, или |осн.>, чтобы подчеркнуть, что оно «основное», наинизшее. Энергию этого состояния легко себе представить. Можно, например, расписать все сигма-векторы через ^σ х , ^σ у и ^σ z , аккуратно подсчитать, каков вклад каждого из них в энергию основного состояния, и все затем сложить. Путь, однако, можно сильно сократить. В гл. 10, § 2 (вып. 8) мы видели, что ^σ i ·^σ j может быть выражено через спин-обменный оператор Паули:

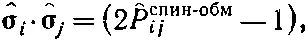(13.3)

где оператор ^P ij спин-обмобменивает спины i -го и j -го электронов. После этой подстановки гамильтониан обращается в

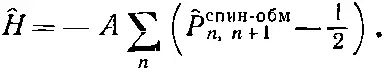(13.4)

Теперь уже легко подсчитать, что происходит в различных состояниях. Например, если и i и j смотрят вверх, то обмен спинами ничего не меняет, так что ^ P ij , действуя на состояние, опять приводят к тому же состоянию, т. е. оно равнозначно умножению на +1. Выражение ^ Р ij - 1/ 2просто равно 1/ 2. (В дальнейшем слова «спин-обм» над Р мы писать не будем.)

В основном состоянии все спины направлены вверх; значит, обмен любой парой спинов приводит опять к исходному состоянию. Основное состояние является стационарным. Если подействовать на него гамильтонианом, получится опять то же состояние, умноженное на сумму чисел —( А /2), по одному на каждую пару спинов. Иначе говоря, энергия системы в основном состоянии составляет по — А /2 на атом.

Теперь подсчитаем энергии некоторых возбужденных состояний. Удобно будет отсчитывать энергии от основного состояния, т. е. в качестве нулевой энергии выбрать энергию основного состояния. Этого можно добиться, добавив к каждому слагаемому в гамильтониане по энергии А /2. Тогда 1/ 2в (13.4) просто заменится единицей. Наш новый гамильтониан будет равен

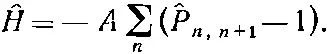(13.5)

При таком гамильтониане энергия низшего состояния равна нулю; спин-обменный оператор равнозначен умножению на единицу (для основного состояния), что сокращается с единицей в каждом слагаемом.

Для описания состояний, отличных от основного, нам понадобится своя совокупность базисных состояний. Удобно подойти к делу так: сгруппировать состояния в соответствии с тем, у скольких электронов спин направлен вниз: у одного ли, у двух и т. д. Конечно, состояний, когда один спин направлен вниз, очень много: он может быть опрокинут, скажем, у атома № 4 или у № 5, или у № 6... И можно, конечно, в качестве базисных состояний выбрать именно такие состояния, обозначив их |4>, |5>, |6>, ... Однако для дальнейшего удобнее, если мы будем отмечать «из ряда вон выходящий атом» (тот, у которого спин направлен вниз) его координатой х . Иначе говоря, мы определим состояние | х 5> как такое, в котором все электроны вращаются спинами вверх, и один только (тот, что возле атома в точке х 5) вращается спином вниз (фиг. 13.1).

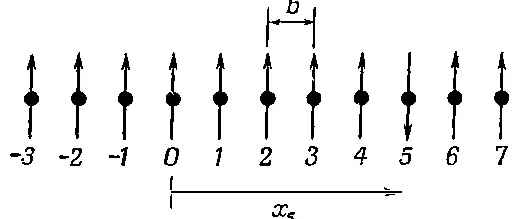
Фиг. 13.1. Базисное состояние |x 5 > системы спинов, расположенных по одной линии. Все спины направлены вверх, а тот, что в х 5 , перевернут.

Вообще, | х n > будет обозначать состояние с одним перевернутым спином, расположенным в координате х n n -го атома.

Как же действует гамильтониан (13.5) на состояние | x 5>? Один из членов гамильтониана это, скажем, — А (^ P 7,8-1). Оператор ^P 7,8обменивает спинами два соседних атома № 7 и № 8. Но в состоянии | x 5> они оба направлены вверх, так что ничего не меняется; ^P 7,8равнозначно умножению на единицу:

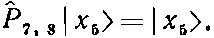
Отсюда следует

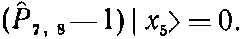
Стало быть, все члены гамильтониана, кроме тех, куда входит атом № 5, дадут нуль. Операция ^P 4,5, действуя на состояние | x 5>, обменивает спинами атом № 4 (со спином вверх) и атом № 5 (со спином вниз). В результате появляется состояние, в котором все спины смотрят вверх, кроме атома в точке 4. Иначе говоря,

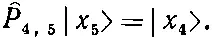
Точно так же

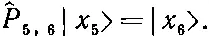
Значит, изо всего гамильтониана выживут только члены — A (^ P 4,5—1) и A (^ P 5,6—1). Действуя на |x 5>, они дадут соответственно — A | x 4>+ A | x 5> и — A | x 6>+ A | x 5>.

В итоге

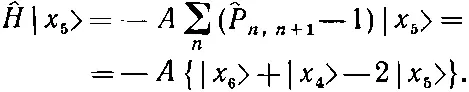(13.6)

Когда гамильтониан действует на состояние | x 5>, то возникает некоторая амплитуда оказаться в состояниях | x 4> и | х 6>. Это просто означает, что существует определенная амплитуда того, что направленный книзу спин перепрыгнет к соседнему атому. Значит, из-за взаимодействия между спинами, если вначале один спин был направлен вниз, имеется некоторая вероятность того, что позднее вместо него вниз будет смотреть другой. При действии на состояние | х n > гамильтониан дает

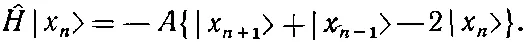(13.7)

Заметьте, в частности, что если взять полную систему состояний только с одним спином-«перевертышем», то они будут перемешиваться только между собой. Гамильтониан никогда не перемешает эти состояния с другими, в которых спинов-«перевертышей» больше. Пока вы только обмениваетесь спинами, вы никогда не сможете изменить общего количества перевертышей. Удобно будет использовать для гамильтониана матричное обозначение, скажем, H n,m ≡< x n |^ H | x m >; уравнение (13.7) эквивалентно следующему: