Ричард Фейнман - Том 3. Квантовая механика

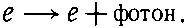(8.16)

Мы не «видим» фотонов внутри электрона до того, как они испустятся, или после того, как они поглотятся, и их «испускание» не изменяет «природы» электрона.

Вернемся к нашей паре протонов. Между ними существует взаимодействие из-за наличия амплитуды А — амплитуды того, что один из протонов испускает нейтральный пион, который проскакивает (с мнимым импульсом) к другому протону и там поглощается. Амплитуда эта опять пропорциональна (8.14), но m π— теперь масса нейтрального пиона. Сходные рассуждения приводят к такому же взаимодействию между двумя нейтронами. А раз ядерные силы (в пренебрежении электрическими эффектами), действующие между нейтроном и протоном, между протоном и протоном, между нейтроном и нейтроном, одинаковы, то мы приходим к заключению, что массы заряженного и нейтрального пионов обязаны быть равны между собой. И экспериментально оказывается, что массы действительно очень близки друг к другу, а небольшая разница между ними — это примерно то, что и следует из поправок на собственную энергию [см. гл. 28 (вып. 6)].

Существуют и другие виды частиц, скажем K-мезоны, которыми могут обмениваться два нуклона. Допустим также и одновременный обмен двумя пионами. Но у всех этих прочих обмениваемых «объектов» масса покоя m x выше массы пиона m π, что приводит к членам в амплитуде обмена, изменяющимся как

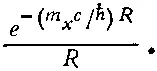
Такие члены с ростом R отмирают быстрее, чем одномезонный член. Сегодня еще никто не знает, как вычислять эти члены с большей массой, но для достаточно высоких значений R выживает только однопионный член. И действительно, те опыты, в которых играет роль только взаимодействие на больших расстояниях, свидетельствуют, что энергия взаимодействия именно такова, как предсказывает теория однопионного обмена.

В классической теории электричества и магнетизма кулоновское электростатическое взаимодействие и излучение света ускоряемым зарядом тесно связаны — оба они вытекают из уравнений Максвелла. Мы видели, что в квантовой теории свет может быть представлен как квантовые возбуждения гармонических колебаний классического электромагнитного поля в ящике. С другой стороны, квантовая теория может быть построена при помощи описания света как частиц — фотонов, подчиняющихся статистике Бозе. В гл. 2, § 5, мы подчеркнули, что обе эти взаимоисключающие точки зрения всегда приводят к одинаковым предсказаниям. Может ли вторая точка зрения быть проведена последовательно и до конца, так чтобы в нее вошли все электромагнитные эффекты? В частности, если мы хотим описать электромагнитное поле полностью на языке бозе-частиц, т. е. фотонов, то чем будет вызвана сила Кулона?

С точки зрения «частиц» кулоновское взаимодействие между двумя электронами вытекает из обмена виртуальными фотонами . Один из электронов испускает фотон [как в реакции (8.16)], который переходит к другому электрону и там поглощается, — та же реакция идет в обратную сторону. Энергия взаимодействия снова дается формулой типа (8.14), но теперь m πзаменяется массой покоя фотона, которая равна нулю. Значит, виртуальный обмен фотоном приводит к энергии взаимодействия, которая меняется просто обратно пропорционально R — расстоянию между электронами — в точности, как нормальная кулоновская потенциальная энергия! В «частичной» (от слова частица) теории электромагнетизма процесс обмена виртуальным фотоном приводит ко всем явлениям электростатики.

В качестве очередной системы с двумя состояниями рассмотрим нейтральную молекулу водорода Н 2. В ней, естественно, труднее разобраться, потому что там имеются два электрона. Мы опять начнем с рассуждений о том, что происходит, когда оба протона достаточно удалены друг от друга. Но теперь к ним следует добавить еще два электрона. Чтобы удобнее было следить за ними, назовем их «электрон a » и «электрон b ». Здесь опять можно себе вообразить два мыслимых состояния. Одна возможность: «электрон а » размазан вокруг первого протона, а «электрон b » — вокруг второго (фиг. 8.4).

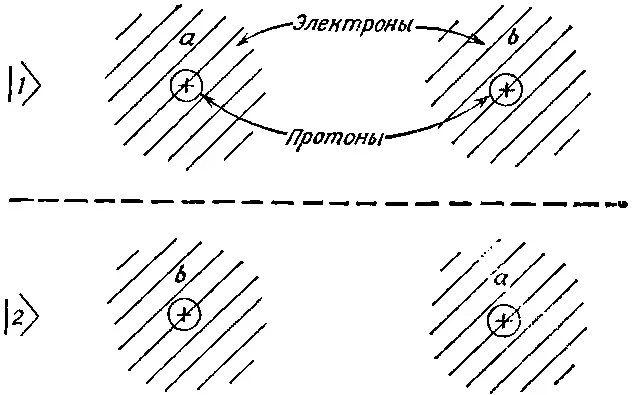
Фиг. 8.4. Совокупность базисных состояний для молекулы Н 2 .

Получаются попросту два атома водорода. Это состояние назовем |1>. Но есть и другая возможность: вокруг первого протона размазан «электрон b », а вокруг второго — «электрон а ». Это состояние обозначим |2>. Из-за симметрии эти две возможности обязаны быть энергетически эквивалентными, но, как мы увидим, энергия системы не есть просто энергия двух атомов водорода.

Нужно заметить, что имеются многие другие возможности. Например, «электрон а » может находиться близ первого протона, а «электрон b » — в другом состоянии вокруг того же протона. Мы не станем рассматривать такой случай, поскольку его энергия заведомо будет больше (из-за сильного кулоновского отталкивания между двумя электронами). Для большей точности, конечно, стоило бы учесть и такие состояния; но уже из рассмотрения одной только пары состояний, показанных на фиг. 8.4, мы узнаем самое главное о молекулярной связи. В этом приближении мы можем описать всякое состояние, задав амплитуду <1|φ> быть в состоянии |1> и амплитуду <2|φ> быть в состоянии |2>. Иными словами, вектор состояния |φ> может быть записан в виде линейной комбинации

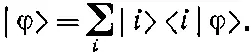
Для дальнейшего, как всегда, предположим, что имеется некоторая амплитуда А того, что электроны могут проходить через промежуточное пространство и обмениваться местами. Эта возможность обмена означает, что энергия системы, как мы наблюдали и в других системах с двумя состояниями, расщеплена. Как и у молекулярного иона водорода, расщепление очень мало, когда расстояние между протонами велико. А когда протоны сближаются, возрастает амплитуда переходов электронов туда-сюда, а вместе с ней растет и расщепление. Убывание энергии в нижнем состоянии означает, что имеется сила притяжения, сближающая атомы. И опять, когда протоны сблизятся особенно тесно, уровни энергии поднимутся вследствие кулоновского отталкивания. В итоге энергии двух стационарных состояний будут меняться с расстоянием так, как показано на фиг. 8.5.