Ричард Фейнман - Том 3. Квантовая механика

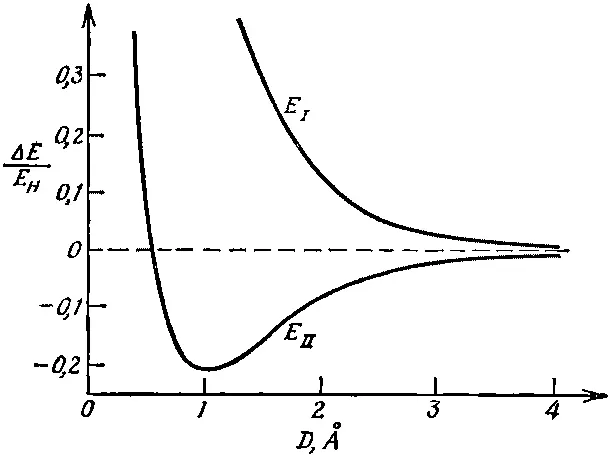
Фиг. 8.3. Уровни энергии иона H 2 + как функция межпротонного расстояния D (E H =13,6 эв).

[На рисунке мы воспроизвели результаты более детальных выкладок. Межпротонное расстояние дано в ангстремах (1Å=10 -8 см ), а избыток энергии над протоном плюс водородным ионом дается в единицах энергии связи атома водорода, так называемых «ридбергах» (13,6 эв ).] Мы видим, что состояние | II > имеет точку минимума энергии — равновесную конфигурацию (условие наинизшей энергии) для иона Н 2 +. Энергия в этой точке ниже, чем энергии отдельно протона и отдельно водородного иона, так что система связана. Отдельный электрон действует так, что скрепляет протоны. Химик назвал бы это «одноэлектронной связью».

Этот род химической связи часто также называют «квантовомеханическим резонансом» (по сходству с двумя связанными маятниками, о котором мы уже говорили). Но звучит это таинственнее, чем оно есть на самом деле; это только тогда «резонанс», когда базисные состояния с самого начала неудачно выбраны, как у нас и было! А если выбрать состояние | II >, вы сразу получите наинизшее энергетическое состояние — и все.

Можно и по-иному объяснить, отчего энергия этого состояния должна быть ниже, чем у протона плюс атома водорода. Представим себе электрон возле двух протонов, удаленных на определенное, но не очень большое расстояние. Вы помните, что электрон возле одиночного протона «размазан» из-за принципа неопределенности. Он ищет равновесия, пытаясь раздобыть энергию пониже (низкую кулоновскую потенциальную энергию) и не оказаться при этом сжатым в пространстве чересчур тесно, что привело бы к высокой кинетической энергии (из-за соотношения неопределенности ΔрΔх≈ℏ). Если же протонов два, то будет больше места, где у электрона может быть низкая потенциальная энергия. Он может размазаться (снижая тем самым свою кинетическую энергию), не повышая при этом своей потенциальной энергии. В итоге его энергия ниже, чем в атоме водорода. Тогда почему же у другого состояния | I > энергия выше? Но заметьте, что это состояние есть разность состояний |1> и |2>. Вследствие симметрии |1> и |2> разность должна иметь нулевую амплитуду того, что электрон окажется на полпути между протонами. Это означает, что электрон немного сильнее ограничен в пространстве, что и приводит к большей энергии.

Следует сказать, что наше приближенное рассмотрение иона H 2 +как двухуровневой системы рассыпается в прах, едва лишь протоны сблизятся до минимума энергии на кривой фиг. 8.3; тогда больше не получается хорошего значения истинной энергии связи. На малых удалениях энергии двух «состояний» на самом деле уже не равны Е 0; требуется более тонкое квантовомеханическое рассмотрение.

Положим, мы теперь заинтересуемся, что случилось бы, если бы вместо двух протонов у нас были два разных объекта, скажем один протон и один положительный ион лития (причем обе частицы по-прежнему имеют по единичному положительному заряду). В этом случае два члена Н 11и H 22в гамильтониане больше не совпадали бы; они были бы совершенно различны. Если бы оказалось, что разность ( H 11- H 22) по абсолютной величине много больше А =- H 12, то сила притяжения стала бы очень слабой. В этом можно убедиться следующим образом.

Если в (8.3) подставить H 12 H 21= A 2, то мы получим

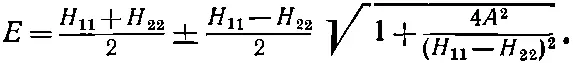
Когда H 11- H 22много больше А 2, корень довольно точно равен

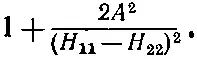
Тогда энергии обращаются в

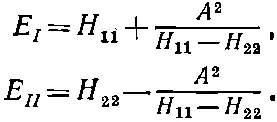(8.8)

Теперь они почти вплотную совпадают с энергиями H 11и H 22изолированных атомов и только чуть-чуть отличаются из-за наличия амплитуды перескока А .

Разность энергий ( Е I - Е II ) равна

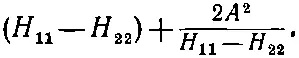
Добавка к расстоянию между уровнями из-за переброса электрона уже не равна 2 А ; она составляет А /( Н 11- Н 22) — часть этой величины (что по предположению много меньше единицы). Кроме того, сама зависимость Е I - Е II от расстояния между ядрами сейчас намного слабее, чем для иона Н + 2: в нее тоже входит множитель А /( Н 11- Н 22). Можно поэтому понять, отчего связь несимметричных двуатомных молекул, как правило, очень слаба.

В нашей теории иона Н + 2мы открыли объяснение механизма, с помощью которого электрон, распределенный между двумя протонами, создает в итоге силу притяжения между ними даже тогда, когда они очень удалены друг от друга. Сила притяжения проистекает от уменьшения энергии системы, вызываемого тем, что у электрона есть возможность прыгать от одного протона к другому. При таких прыжках система переходит от конфигурации атом водорода — протон к конфигурации протон — атом водорода и обратно. Процесс символически можно записать так:

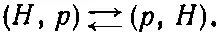
Сдвиг энергии, вызываемый этим процессом, пропорционален амплитуде А того, что электрон с энергией -W H(его энергия связи в атоме водорода) может от одного протона перейти к другому.

При больших расстояниях R между протонами электростатическая потенциальная энергия электрона близка к нулю почти во всем том пространстве, которое он вынужден преодолеть, делая прыжок. Так что в этом пространстве электрон движется почти как свободная частица в пустом пространстве, но обладая при этом отрицательной энергией! В гл. 1 [уравнение (1.7)] мы видели, что амплитуда для частицы определенной энергии перейти с одного места на другое, удаленное на расстояние r , пропорциональна

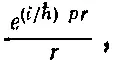
где р — импульс, отвечающий заданной энергии. В теперешнем случае (применяется нерелятивистская формула) р определяется из выражения

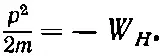(8.9)

А это значит, что р —число мнимое: