Ричард Фейнман - Том 3. Квантовая механика

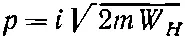
(другой знак перед корнем приводит к абсурду).

Стало быть, следует ожидать, что амплитуда А для иона Н 2 +будет меняться как

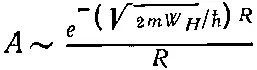(8.10)

при больших расстояниях R между протонами. Сдвиг энергии, вызываемый электронной связью, пропорционален А ; значит, существует сила, сближающая два протона, которая пропорциональна (при больших R ) производной от (8.10) по R .

Наконец, для полноты следует заметить, что в одноэлектронной системе с двумя протонами есть еще один эффект, который тоже приводит к зависимости энергии от R . Мы пока им пренебрегали, поскольку он обычно не очень важен, за исключением как раз тех больших расстояний, на которых энергия обменного члена А убывает экспоненциально до очень малых величин. Новый эффект, о котором мы говорим, — это электростатическое притяжение протона к атому водорода, возникающее по той же причине, по какой любой заряженный предмет притягивает к себе незаряженный. «Голый» протон создает электрическое поле ℰ (изменяющееся как 1/ R 2) возле нейтрального атома водорода. Атом становится поляризованным, приобретая наведенный дипольный момент μ, пропорциональный ℰ. Энергия диполя есть μℰ,т. е. пропорциональна ℰ 2, или 1/ R 4. Значит, в выражении для энергии системы существует член, убывающий как четвертая степень расстояния (это поправка к e 0). Эта энергия спадает с расстоянием медленнее, чем сдвиг А , даваемый формулой (8.10). На каких-то больших расстояниях R член с R 4становится важнейшим, определяющим изменение энергии с R , и поэтому единственной оставшейся силой. Заметьте, что электростатический член для обоих базисных состояний имеет один знак (раз сила притягивает, то энергия отрицательна), а потому и для обоих стационарных состояний его знак один и тот же, в то время как член электронного обмена А для двух стационарных состояний дает разные знаки.

Мы видели, что система, составленная из атома водорода и протона, вследствие обмена одним электроном обладает энергией взаимодействия, которая на больших расстояниях R меняется как

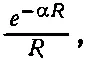(8.11)

где a =√(2 mW H )/ ℏ . (Обычно говорят, что происходит обмен «виртуальным» электроном, когда, как в нашем случае, электрон вынужден перепрыгивать через ту область, где его энергия оказалась бы отрицательной. Конкретнее говоря, «виртуальный обмен» означает, что явление предполагает квантовомеханическую интерференцию между состоянием без обмена и состоянием с обменом.)

А теперь следует задать такой вопрос: не может ли быть, что и силы, действующие между другими частицами, имеют сходное происхождение? Что, к примеру, можно сказать о ядерной силе, действующей между нейтроном и протоном или между двумя протонами? Пытаясь объяснить природу ядерных сил, Юкава предположил, что сила, действующая между двумя нуклонами, вызывается сходным обменным эффектом, только в этом случае из-за виртуального обмена не электроном, а какой-то новой частицей, которую он назвал «мезон». Сегодня мы бы отождествили мезон Юкавы с π-мезоном (или «пионом»), возникающим в высокоэнергетических столкновениях протонов или других частиц.

Посмотрим для примера, какого рода силы возникнут от того, что протон и нейтрон обменяются положительным пионом (π +), имеющим массу m π. Как атом водорода Н 0может, отказавшись от электрона е -, превратиться в протон р +

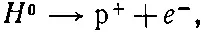(8.12)

точно так же протон р +может перейти в нейтрон n 0, отказавшись от π +-мезона:

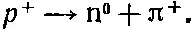(8.13)

Значит, если у нас есть протон (в точке а ) и нейтрон (в точке b ), разделенные расстоянием R , то протон может стать нейтроном, испуская π +-мезон, который затем поглощается нейтроном в точке b , обращая его в протон. И имеется энергия взаимодействия системы из двух нуклонов и одного пиона, зависящая от амплитуды А пионного обмена, как это было с электронным обменом в ионе Н + 2.

В процессе (8.12) энергия атома Н 0(если вычислять ее нерелятивистски, опуская энергию поля электрона W H) меньше энергии протона на величину mc 2, так что кинетическая энергия электрона отрицательна — или импульс мнимый [см. уравнение (8.9)]. В ядерном процессе (8.13) массы протона и нейтрона почти равны, так что полная энергия π +-мезона окажется равной нулю. Соотношение между полной энергией Е и импульсом р пиона с массой m πтаково:

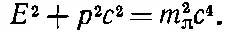
Раз Е равно нулю (или по крайней мере пренебрежимо мало по сравнению с m π), то импульс опять выходит мнимый:

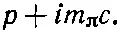
Повторяя знакомые нам уже рассуждения, с помощью которых мы вычисляли амплитуду того, что связанный электрон проникнет через барьер в пространстве между двумя протонами, мы получаем для ядерного случая амплитуду обмена А , которая — при больших R — будет вести себя как

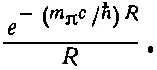(8.14)

Энергия взаимодействия пропорциональна А и, значит, меняется таким же образом. Мы получаем изменение энергии в форме так называемого потенциала Юкавы между двумя нуклонами. Кстати, ту же формулу мы получили раньше прямо из дифференциального уравнения для движения пиона в пустом пространстве [см. гл. 28 (вып. 6), уравнение (28.18)].

Следуя той же линии рассуждений, можно попытаться прикинуть взаимодействие двух протонов (или двух нейтронов), происходящее от обмена нейтральными пионами (π 0). Основной процесс теперь таков:

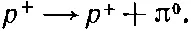(8.15)

Протон может испустить виртуальный π 0, оставаясь после этого все еще протоном. Если протонов два, то протон № 1 может испустить виртуальный π 0, который поглотится протоном № 2. В конце остается опять пара протонов. Это немного не то, что было в случае иона H 2 +. Тогда Н 0переходил после испускания электрона в другое состояние — в протон. Теперь же мы предполагаем, что протон может испускать π 0, не меняя своего характера. Такие процессы и впрямь наблюдаются в высокоэнергетических столкновениях. Процесс аналогичен тому, как электрон, испуская фотон, остается все же электроном: