Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]

Традиционные математические методы, основанные на ручных расчетах, никак не в состоянии решить даже упрощенные варианты этой задачи. Быстрые компьютеры с большими объемами памяти аппроксимируют задачу при помощи численных методов, а затем проводят множество вычислений методом «грубой силы», чтобы получить приближенный ответ. В большинстве моделей сталкивающиеся тела рассматриваются как капли липкой жидкости, способные как разбиваться на более мелкие капли, так и сливаться в более крупные. Первоначальные капли имеют размеры планет; капли, на которые они дробятся, меньше, но только по сравнению с планетами. На самом деле они по-прежнему довольно велики.

Стандартная модель динамики жидкости восходит к XVIII веку, к Леонарду Эйлеру и Даниилу Бернулли. Она формулирует физические законы течения жидкости в виде уравнения в частных производных, описывающего, как скорость жидкости в каждой точке пространства изменяется со временем в ответ на действующие силы. Такие уравнения не решаются в формульном виде, за исключением простейших случаев, но разработаны очень точные вычислительные методы их решения. Серьезный вопрос здесь — природа модели, которая в принципе требует исследовать скорость жидкости в каждой точке некоторой области пространства. Однако даже компьютеры не в состоянии произвести бесконечное число расчетов, поэтому мы «дискретизируем» уравнение: аппроксимируем его связанным уравнением, в котором задействовано лишь конечное число точек. В простейшем методе в качестве репрезентативной выборки для всего объема жидкости используются узлы некоторой решетки, в которых и отслеживается динамика изменения скорости. При достаточно частой решетке аппроксимация получается неплохая.

К несчастью, такой подход не слишком годится для сталкивающихся капель, потому что при разбивании капли поле скорости получает разрывы. На помощь приходит хитроумный вариант метода решетки. Он работает даже тогда, когда капли разбиваются на более мелкие или, наоборот, объединяются в более крупные. Этот метод, известный как гидродинамика сглаженных частиц, разбивает жидкость на соседние «частицы» — крохотные области. Но вместо того, чтобы использовать фиксированную решетку, мы следуем за частицами и следим, как они отзываются на действующие силы. Если соседние частицы движутся примерно с одинаковой скоростью и в одном направлении, они находятся в одной капле и останутся в ней. Но если соседние частицы направляются в совершенно разных направлениях или имеют существенно разные скорости, то капля разбивается на более мелкие.

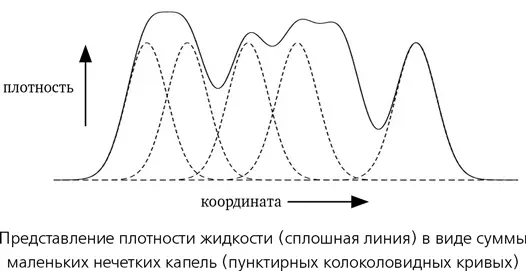
Математика добивается такого эффекта, «сглаживая» каждую частицу и превращая ее в своего рода мягкий пушистый шарик (называется это сферической перекрывающейся кернфункцией), а затем накладывая эти шарики друг на друга. Каждый шарик может быть представлен своей центральной точкой, и нам необходимо рассчитать, как эти точки движутся с ходом времени. Математики называют уравнение такого рода задачей n тел, где n — число точек, или, что то же самое, число пушистых шариков.

Все это очень хорошо, но задача n тел трудна. Кеплер исследовал задачу двух тел — орбиту Марса — и сделал вывод о том, что она представляет собой эллипс. Ньютон доказал математически, что когда два тела движутся под воздействием гравитации, убывающей по обратно-квадратичному закону, то оба они движутся по эллипсам вокруг общего центра масс. Но попытавшись разобраться в задаче трех тел — в базовом случае это Солнце, Земля и Луна, — математики XVIII–XIX веков обнаружили, что это далеко не такая аккуратная и упорядоченная задача. Даже громадная формула Делоне представляет собой всего лишь аппроксимацию. На самом деле орбиты тел в этой задаче, как правило, хаотичны — очень и очень нерегулярны — и никакими красивыми формулами или классическими геометрическими кривыми не описываются. Подробнее о хаосе можно прочитать в главе 9.

Чтобы реалистично смоделировать планетарное столкновение, число пушистых шариков должно быть велико — скажем, тысяча, а еще лучше миллион. Компьютеры умеют оперировать большими числами, но здесь n говорит не о суммах, которые появляются в вычислениях; n характеризует сложность сумм. А мы здесь сталкиваемся с «проклятием размерности», где размерность системы равна количеству чисел, необходимых для ее описания.

Предположим, мы используем миллион шариков. Чтобы определить состояние каждого шарика, требуется шесть чисел: три для координат в пространстве, еще три для компонент скорости. Это шесть миллионов чисел — только для того, чтобы определить состояние системы в произвольный момент. Мы хотим воспользоваться законами механики и гравитации, чтобы предсказать будущее движение системы. Эти законы представляют собой дифференциальные уравнения, определяющие состояние системы на крохотный шаг вперед, в будущее, при известном текущем состоянии. При маленьком шаге по времени — пусть это будет, скажем, секунда — результат получится очень близким к реальному состоянию системы в будущем. Так что теперь нам придется вычислить сумму для шести миллионов чисел. Точнее говоря, нам придется получить шесть миллионов сумм для шести миллионов чисел — по одному суммированию на каждое число, необходимое для описания будущего состояния. Так что сложность наших расчетов составит шесть миллионов, умноженные на шесть миллионов, а это 36 триллионов. И посчитав все это, мы узнаем лишь, каким будет следующее состояние, через секунду после нынешнего. Повторив расчет еще раз, мы узнаем, что произойдет через две секунды, и т. д. Чтобы выяснить, что произойдет через тысячу лет, нам нужно просчитать период примерно в 30 миллиардов секунд, и сложность расчетов при этом составит 30 миллиардов, умноженные на 26 триллионов — около 10↑ 24, или один септиллион.

И это еще не самое худшее. Хотя каждый отдельный шаг, возможно, является хорошей аппроксимацией, шагов так много, что даже самая крохотная ошибка может значительно вырасти; кроме того, объемные вычисления занимают много времени. Если бы компьютер мог рассчитывать один шаг в секунду, то есть работал бы «в реальном времени», на расчеты потребовалось бы не меньше тысячи лет. Только суперкомпьютер способен хотя бы приблизиться к таким параметрам вычислений. Единственный выход — найти другой, более хитрый способ проводить вычисления. На ранних этапах столкновения действительно может потребоваться короткий шаг по времени — скажем, одна секунда, — потому что возникнет страшная путаница и все будет очень сложно. Позже шаг по времени можно сделать более длинным, результат, вероятно, останется приемлемым. Более того, как только две точки разойдутся на достаточно большое расстояние, сила взаимодействия между ними станет настолько маленькой, что ею, скорее всего, можно вообще пренебречь. Наконец, именно здесь можно получить наибольший выигрыш — весь расчет можно упростить, организовав его более хитроумным способом.