Айзек Азимов - Популярная физика. От архимедова рычага до квантовой механики

Вращательное движение способно совершаться любым из двух зеркально отраженных способов. Если смотреть из некоторого фиксированного положения, то колесо может выглядеть вращающимся «по часовой стрелке», то есть в том же направлении, в котором двигаются стрелки часов. Но с другой стороны, оно может двигаться «против часовой стрелки», то есть в сторону, противоположную движению стрелок часов [25] Важно отметить фразу «из некоторого фиксированного положения», потому что термины «по часовой стрелке» и «против часовой стрелки» не являются абсолютными. Колесо может казаться поворачивающимся по часовой стрелке, когда вы смотрите на него с одной стороны, но если вы переходите на противоположную сторону, то рассматриваемое колесо будет казаться вам поворачивающимся против часовой стрелки. То же самое истинно, если мы говорим о поступательном движении, что тело двигалось «влево» или «право» или «к» и «от». Все эти термины имеют значение только тогда, когда вы учитываете ваше собственное расположение. Однако если вы говорите относительно «севера», «юга», «востока» или «запада», то эти термины устанавливаются относительно Земли и не зависят от вашего собственного расположения. . Поэтому об угловой скорости можно говорить, учитывая не только величину, но также и направление. (Что касается скоростей, включаемых в поступательное движение, то о них можно говорить как о «линейных скоростях», так как движение тут происходит скорее по линии, чем по углу.)

Физики используют другую единицу измерения вращательной скорости — радиан. Это угол, который отображает на окружности дугу, равную по длине радиусу круга. Длина окружности равна π, умноженному на диаметр окружности [26] Греческая буква π используется, чтобы представить отношение длины окружности (с) круга к его диаметру (d); другими словами, c/d = π). И хотя каждый круг может иметь различные значения с и d, отношение этих двух величин — c/d — всегда одно и то же для всех кругов. Поэтому π — константа, ее приблизительное значение равно 3.14159. , то есть 2π умножить на радиус круга. Поэтому длина окружности равна 2πr , умноженным на длину дуги, обозначенной одним радианом. Один полный оборот заключает в себя прохождение одной полной длины окружности, то есть один оборот равняется 2π радианам, или 360°. Из этого следует, что один радиан равняется 360°/2π, или, так как к равняется 3,14159, один радиан примерно равен 57,3° (1 рад = 57,3°).

Угловая скорость часто обозначается греческой буквой ω («омега»), так как это — греческий эквивалент латинской буквы v, обычно используемой для обозначения линейной скорости.

Для любой данной точки на вращающемся теле угловая скорость может быть приведена к линейной скорости. Линейная скорость зависит не только от угловой скорости, но также и от расстояния, на котором находится рассматриваемая точка от центра вращения (r). Если для той же самой угловой скорости удвоить расстояние от точки до центра вращения, то линейная скорость точки также удвоится. В таком случае можно сказать, что:

Это уравнение абсолютно корректно, когда ω измеряется в радианах в единицу времени. Например, если угловая скорость — один радиан в секунду, то за одну секунду данная точка, расположенная на окружности колеса, проходит дугу, равную ее расстоянию от центра, и v = r. Εсли ω равняется 2 радианам в секунду, то v = 2r и так далее.

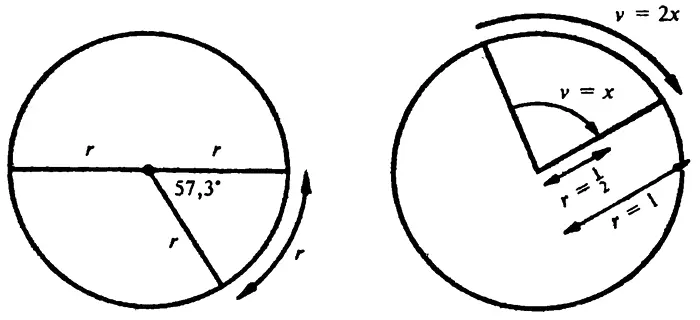
Если бы мы измеряли ω в оборотах в единицу времени, то уравнение 6.4 можно было бы прочитать как (v = 2πrω), а если бы мы измеряли ее в градусах в единицу времени, то это же уравнение можно было бы прочитать как v = rω/57,3. Это — пример того, как единица измерения, которая на первый взгляд может показаться имеющей странную и неудобную размерность, оказывается весьма полезной, потому что она позволяет выразить отношения между величинами с максимальной простотой.

Для того чтобы привести тело, находящееся в состоянии покоя, в поступательное движение, требуется приложить к нему силу. Но при некоторых условиях сила может вместо этого вызвать вращательное движение тела. Предположим, например, вы прибили гвоздем один конец доски к деревянному основанию. Если вы теперь толкнете доску, то она не будет двигаться в поступательной манере движения, так как один конец ее закреплен. Вместо этого доска начнет совершать вращательное движение вокруг зафиксированного конца.

Сила, которая вызывает такое вращательное движение, называется крутящим моментом («torque» — от латинского слова, означающего «вращать»). Если мы продолжим использовать греческие буквы для обозначения элементов вращательного движения, мы можем обозначить крутящий момент греческой буквой τ («tau» — «тау»), которая является эквивалентом латинской буквы «t» (от латинского «torque» — очевидно).

Данная сила не всегда вызывает тот же самый крутящий момент. В случае упомянутой доски величина крутящего момента зависит от расстояния между точкой, к которой приложена сила, и фиксированной точкой. Сила, приложенная непосредственно к фиксированной точке, не будет вызывать крутящий момент. По мере отступа от этой точки данная сила произведет все более быстрое вращение и поэтому вызовет все больший и больший крутящий момент. Фактически крутящий момент равен силе (f), умноженной на расстояние (r):

В прошлом о крутящем моменте говорили как о «моменте силы», но эта фраза теперь вышла из употребления. Крутящий момент может быть вызван не только в случае, когда какая-то часть тела зафиксирована в пространстве, но даже тогда, когда все тело способно свободно перемещаться.

Рассмотрим тело, обладающее массой, но состоящее из одной-единственной точки. Такое тело может подвергнуться только поступательному движению. Вращающееся тело, в конце концов, крутится относительно некоторой точки (или линии); если эта точка — все, что существует, и нет ничего еще, что могло бы вращаться, возможно только линейное движение. Зато к таким точечным массам наиболее просто применить законы движения.

Однако в реальной Вселенной не существует никаких точечных масс. Все реальные тела, обладающие массой, могут расширяться. Однако можно показать, что в некоторых случаях такие реальные тела ведут себя так, как будто вся их масса сконцентрирована в какой-то одной точке. Точка, в которой эта кажущаяся концентрация может быть найдена, называется «центром масс» тела. Если тело симметрично по форме и однородно по плотности или имеет плотность, которая изменяется симметричным образом, центр массы совпадает с геометрическим центром тела. Например, Земля, по существу, сферическое тело, но в то же время оно неравномерно плотно, плотность Земли — наибольшая в центре, и эта плотность уменьшается одинаково во всех направлениях, по мере приближения к поверхности. Центр масс Земли поэтому совпадает с ее геометрическим центром, и именно к этому центру и направлена сила тяжести.