Айзек Азимов - Популярная физика. От архимедова рычага до квантовой механики

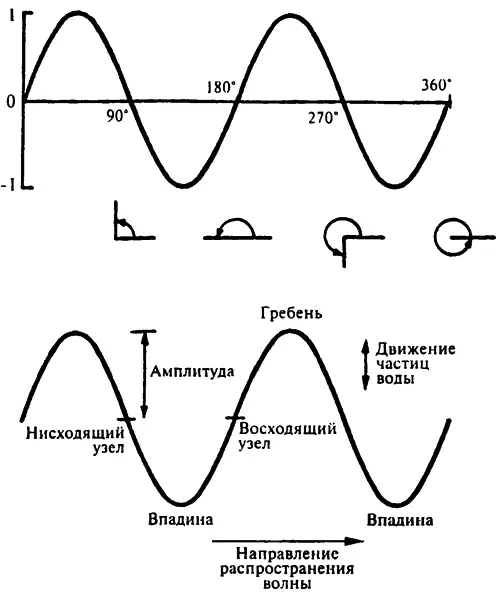
Точка, в которой возмущение является наибольшим в восходящем направлении (+1 на синусоиде), называется «гребнем» волны, а точка, в которой оно является наименьшим в нисходящем направлении (–1 на синусоиде), называется «впадиной» [49] Авторские термины. (Примеч. пер.) . Между гребнем и впадиной находятся точки, где вода на мгновение находится на «нулевом» уровне, то есть она уже не поднимается, но еще не опускается (точка 0 на синусоиде); такие точки называются «узлами». В жидкостных волнах имеются два вида таких узлов, поскольку вода проходит через узел по мере продвижения к впадине и по мере продвижения к вершине гребня. Мы можем назвать их «восходящие узлы» и «нисходящие узлы» (позаимствовав термины, используемые для аналогичной цели в астрономии). Вертикальное расстояние от узла до гребня волны или до впадины называется ее «амплитудой».

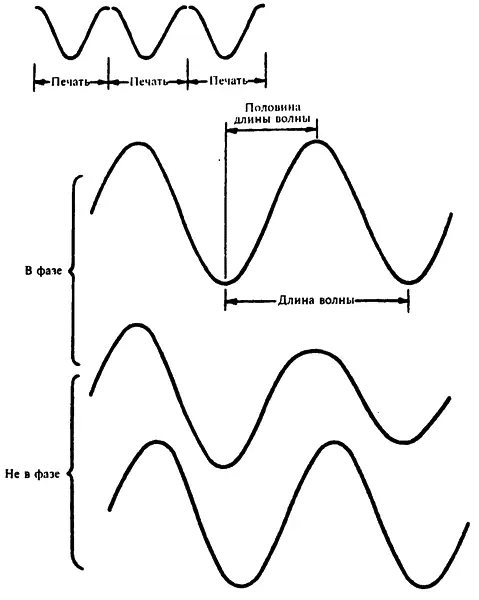
Если две или более точки занимают одни и те же взаимные положения в синусоиде, то про такие точки говорят, что они находятся в фазе. Например, все точки на различных вершинах одной волны находятся в фазе, так же как и все точки на различных впадинах. Все восходящие узлы находятся в фазе; все нисходящие узлы находятся в фазе. Все точки, находящиеся на одном расстоянии между восходящим узлом и гребнем, находятся в фазе и так далее. Если существуют две таких волны, у которых в любой момент времени каждый гребень совпадает в пространстве или по форме с гребнем другой в тот же самый момент времени, то говорят, что части этих двух волн находятся в фазе. Возможен даже такой случай, что обе волны могут быть в фазе на всем своем протяжении таким образом — гребень в гребень и впадина во впадину.

Естественно было бы назвать точки, расположенные на одной и той же волне и находящиеся не в фазе, точками «не в фазе». И пару волн, у которых гребень в данный момент времени не совпадает с гребнем другой волны, — волнами «не в фазе».

Синусоида может рассматриваться как состоящая из одной специфической маленькой части, которая повторяет себя неопределенное число раз. Например, часть синусоиды от одного гребня до следующего может быть воспроизведена в виде печати, и если вам захочется, то полную синусоиду можно воспроизвести, отпечатывая одну эту часть, присоединяя печать справа к окончанию предыдущей, к ее окончанию — следующую и так далее. Тот же самый эффект мы получим, если возьмем часть синусоиды от впадины до впадины, или от восходящего узла до восходящего узла, или от нисходящего узла до нисходящего узла и так далее. Мы всегда можем получить соответствующий шаблон, если возьмем участок от одной точки на синусоиде до второй, находящейся с ней в фазе.

Для любой взятой синусоиды расстояние от некоторой произвольной точки до следующей такой же — величина постоянная. Эта длина (для простоты возьмем длину от гребня до гребня) определяет «длину волны». Длина волны обычно обозначается греческой буквой «лямбда» (λ).

Если узлы не отличаются друг от друга (а в физике они обычно не различаются), то расстояние между последовательными узлами равно половине длины волны (полуволне). Если восходящий узел одной волны при наложении совпадает с нисходящим узлом другой волны (такое иногда тоже случается), то говорят, что волны находятся «в противофазе», но расстояние между последовательными узлами все равно составляет половину длины волны.

В данной волне гребень двигается по направлению наружу по поверхности воды (хотя вода непосредственно, хочу повторить, не двигается наружу вместе с ним); расстояние, которое он проходит за одну секунду, называется скоростью распространения волны.

Давайте представим себе, что скорость распространения данной волны составляет десять метров в секунду и что длина волны (то есть расстояние от гребня до гребня) равняется двум метрам. Если мы обратим наше внимание на некоторую точку на поверхности воды, мы увидим, что в ней через некоторое время образуется гребень. Он начинает перемещаться, и, когда он переместится на два метра по направлению наружу, его место займет второй гребень, еще два метра вперед, и в точке появится третий гребень и так далее. После того как пройдет одна секунда, первоначальный гребень окажется на расстоянии в десять метров, а его место займет пятый гребень (10 разделить на 2).

Количество гребней (или количество впадин, восходящих узлов, нисходящих узлов или любых других последовательных точек в фазе), которые прошли через данную точку за одну секунду, называется «частотой колебаний» волны. Частота обычно обозначается греческой буквой «ню» (ν).

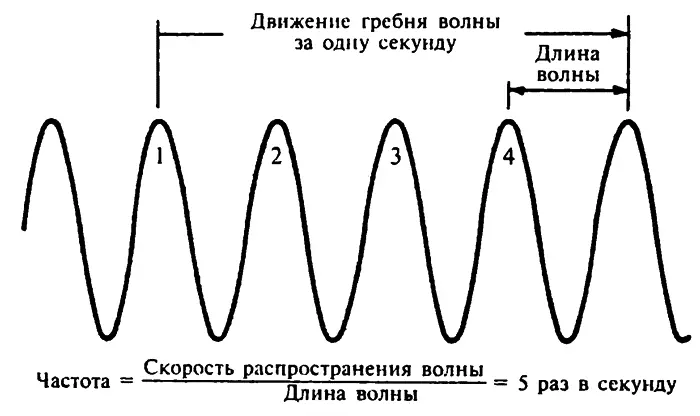
Из того, что я только что сказал, должно быть ясно, что скорость распространения волны, поделенная на ее длину, равняется частоте ее колебаний, то есть:

Единицы измерения скорости в системе МКС — метры в секунду, единицы измерения длины волны — метры. Поэтому единицы измерения частоты получаются равными (м/с)/м, или 1/с. Поскольку в алгебре 1/a называется величиной, «обратной» a, величину 1/с иногда называют «обратными секундами». Более часто, конечно, мы просто говорим «в секунду». Например, частота упомянутой выше волны может быть записана как 5/с и читаться как «5 раз в секунду» или как «5 обратных секунд».

Еще на сравнительно ранней стадии развития поисков знания у исследователей возникли мысли о том, что звук представляет собой один из видов волнового движения. Впервые эксперименты со звуком начали проводить еще древние греки, и замечательно то, что созданная ими для изучения звука ветвь физики с самого начала развивалась в правильном направлении даже с точки зрения современных критериев.

Уже в VI столетии до н.э. Пифагор Самосский изучал звук, который издают струны. Как мы можем заметить, если струну «ущипнуть», то она начинает вибрировать. Движения струны выглядят как размытое пятно, но даже в этом случае можно получить некоторые полезные факты, связанные со звуком. Похоже на то, что ширина этого размытого пятна, созданного движением струны, соответствует громкости звука. По мере того как вибрация утихает, а ширина пятна сужается, звук становится менее громким. А когда вибрация прекращается, не важно — естественным замедлением или резкой остановкой струны рукой, — звук также прекращается. Кроме того, легко выяснить, что чем короче натянутая струна, тем более быстро она вибрирует, и более быстрая вибрация, как кажется, производит более пронзительный звук; в то же время более длинная струна, как кажется, вибрирует медленнее, а звук издает более низкого тона.