Айзек Азимов - Популярная физика. От архимедова рычага до квантовой механики

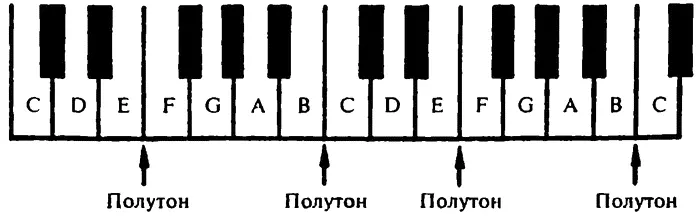
Желательно быть способным играть гамму от любой точки на клавиатуре фортепьяно, например, для того, чтобы приспособить диапазон фортепьяно к конкретному человеческому голосу. По этой причине в каждую октаву вставлены пять черных нот, расстояния между «белыми» клавишами и «черными» клавишами равны одному полутону, что позволяет разбить любую октаву на пять больших интервалов. Это позволяет нам сохранить привычную последовательность двух (CD, DE) и трех тонов (FG, GA, АВ) — тон, тон, полутон, тон, тон, тон, полутон — по всей клавиатуре. Теперь можно начинать играть гамму с любой клавиши фортепьяно, не важно — с черной или с белой; не забывайте только выбирать ноты тщательно и нажимать иногда черную, а иногда белую. И только если вы начинаете с С, вы можете сыграть всю гамму, всего лишь нажимая последовательно белые клавиши.

Именно по той причине, что С оказывается естественной до, игра в «ключе С» является самой простой для начинающих (главным образом — только белые клавиши). До первой октавы [57] У нас принято отсчитывать интервалы от до большой октавы, частота которой равна 64/с, то есть частота до первой октавы равна 256/с. Однако в музыке более важной является не частота звука, а точное соотношение между звуками, то есть величина интервала. Поэтому данная разница не имеет большого значения. (Примеч. пер.) является специфической нотой, которая находится примерно в середине клавиатуры фортепьяно, частота этой ноты равна 264/с [58] Физики часто используют для С частоту 256/с, потому что, такое число является степенью числа 2. Оно представляет собой 2x2x2x2x2x2x2x2, или 2 8 . .

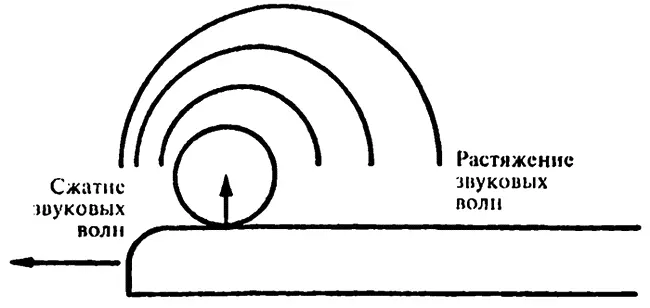
Высота тона изменяется, если источник звука перемещается относительно слушателя. Предположим, что стоящий вдалеке поезд издает гудок, который имеет частоту 344/с. В этом случае, когда звуковая волна достигает нас, в нашу барабанную перепонку каждую секунду будут ударять 344 комбинации сжатия/разрежения. Поскольку звук (при комнатной температуре) двигается со скоростью 344 метра в секунду, последовательные области сжатия будут располагаться на расстоянии одного метра.

Предположим теперь, что поезд начинает быстро двигаться по направлению к нам со скоростью 34,4 метра в секунду (75,8 мили в час), или, иначе, — со скоростью, равной одной десятой скорости звука. Он все еще продолжает издавать гудок. Одна область сжатия перемещается перед ним; ко времени, когда она переместилась на один метр, испускается другая область сжатия. Однако к этому времени поезд продвинулся вперед на десятую часть метра, и вторая область сжатия будет находиться на расстоянии только 0,9 метра позади первой. Если поезд движется с постоянной скоростью, то же самое происходит и со всеми остальными последовательными областями сжатия. По этой причине наших барабанных перепонок достигает сначала первая область, а затем — следующая, но звуковые волны исходят от движущегося поезда, а потому вторая волна достигнет наших барабанных перепонок на 0,1 секунды раньше, то есть до нас доходит 344/0,9, или 382 колебания. Человек, едущий на поезде и поэтому перемещающийся вместе с источником звука, получает за одну секунду все те же 344 области сжатия. Отношение 382:344 близко к 9:8, так что звук гудка поезда представляется более пронзительным для человека, наблюдающего подход поезда, чем для человека, который едет на поезде, и разница составляет почти целый тон.

С другой стороны, если поезд удаляется от слушателя, то за то время, когда первая область сжатия переместилась на метр к слушателю, возникает новая область, поезд отдалится на десятую часть метра и расстояние между двумя областями сжатия будет 1,1 метра. Частота звука составит тогда 344/1,1, или 312 раз в секунду. Теперь это ниже почти на целый тон, чем было бы слышно человеку на поезде.

Если бы мы стояли на перроне, то звук гудящего и проносящегося мимо нас поезда изменился бы внезапно: от частоты 382/с по мере приближения и прохождения к частоте 312/с по мере удаления. Это явление называется эффектом Доплера, названным так в честь австрийского физика Иоганна Кристиана Допплера (1803–1853), который первым изучил и дал правильное объяснение данному эффекту в 1842 году.

Высота тона также может изменяться и гораздо более тонким способом. Одна и та же нота, сыгранная с одной и той же громкостью на фортепьяно, скрипке или кларнете, звучит для нас по-разному. При наличии хотя бы минимального опыта мы можем легко определить, на каком из инструментов была сыграна данная нота. Эта разница в звуках, которые являются идентичными по высоте и громкости, определяется разницей в «качестве», или «тембре», звука.

Чтобы объяснить это, мы должны учесть, что колебания струны или любого другого устройства, производящего звук, на самом деле более сложные, чем я их описал. Струна, например, может действительно вибрировать целиком, чтобы создать вибрацию и поэтому звуковую волну данной частоты. По аналогии с поперечной волной это была бы простая синусоида и то, что называется «основным тоном». Именно основной тон мы обычно и имеем в виду, когда говорим о частоте какой-то специфической ноты.

Однако струна может вибрировать так же, как состоящая из двух половин: одна половина смещается вправо, в то время как другая половина смещается влево, и наоборот; средняя же точка струны, разграничивающая эти две половины, выступает в роли неподвижного узла. Каждая из половин струны вибрирует с частотой в два раза большей, чем частота целой струны, так что звучащий тон будет по высоте в два раза выше, чем основной тон. Струна может также вибрировать с периодом в три, четыре, пять и так далее раз меньшим, производя при этом тон в три, четыре, пять и так далее раз более высокий, чем основной. Все эти ноты более высоких частот называются «обертонами». Основной тон и различные обертоны звучат одновременно, и в реальности движение струны является их комбинацией. Основной тон остается доминирующим, но обертоны добавляют свои формы волны, и поэтому окончательная форма волны является гораздо больше сложной, чем простая синусоида. Кроме того, при различных условиях в струнах (пока мы не будем говорить о других источниках звука) обертоны могут обладать различной громкостью звука, в некоторых случаях обертон может даже звучать громче, чем основной тон, так что окончательная форма звуковой волны будет различной для разных инструментов. Разница в звучании является вполне достаточной, чтобы мы могли ее заметить при помощи наших барабанных перепонок.