Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

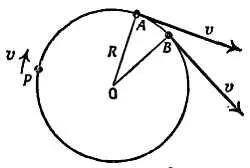
Фиг. 102. Векторы скорости.

Вывод формулы а = v 2/ R .

По мере движения тело Р изменяет свою скорость от ( vвдоль АТ ) до ( v вдоль BT '). Для определения изменения скорости построим векторную диаграмму. Перенесем эти два вектора в общую точку X и проведем линию XY , представляющую вектор скорости vв точке А , и линию XZ , представляющую вектор скорости vв точке В .

Тогда XY будет «старая скорость», a XZ — «новая скорость». Каково же изменение скорости? Какой вектор следует добавить к старому вектору скорости для получения нового вектора скорости?

Такое изменение показано с помощью отрезка YZ , представляющего собой вектор и обозначенного Δ v на фиг. 103.

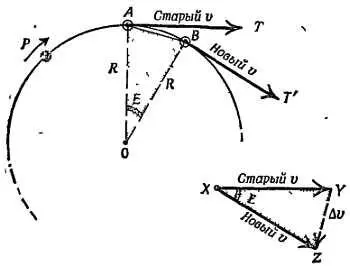
Фиг. 103. Изменение скорости.

Скорости направлены по касательным, перпендикулярным радиусам, поэтому треугольник ОАВ подобен угольнику XYZ векторной диаграммы

Тогда ( Старый вектор v) + Δ v путем сложения векторов дает ( Новый вектор v).

Чтобы увидеть, куда направлен вектор Δ v , изобразим заново первоначальный рисунок, но таким образом, чтобы векторы v сместились вдоль своих направлений до совмещения их точек приложения в точке С (фиг. 104).

Фиг. 104. Направление изменения скорости.

Тогда мы можем рассматривать точку С в качестве X , провести из этой точки старый вектор vи новый вектор vи провести также вектор Δ v . Вектор Δ vпараллелен линии СО , проведенной из точки С в центр круга О . Если поместить точку В очень близко к А , то Δ vбудет направлен по радиусу от АВ к центру. Вектор Δ v— это вектор скорости, направленный к центру круга.

Ускорение возникает только при изменении скорости [79] Начиная с этого момента мы больше не будем рассматривать v и Δ v в качестве векторов и не будем обозначать их жирным шрифтом, так как мы переходим к вычислению абсолютной величины ускорения, используя скорость v , которая является величиной вектора скорости, и Δ v , которое является величиной изменения вектора скорости. Будем помнить, однако, что ускорение имеет направление, совпадающее с направлением вектора Δ v . . Рассчитаем это ускорение путем деления величины изменения скорости Δ v на интервал времени Δ t , за который это изменение происходит. Время Δ t равно времени прохождения телом Р расстояния по орбите между точками А и В со скоростью v . Фактически скорость v есть дуга 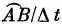. Для выражения Δ v /Δ t через v и R и т. д. мы вынуждены обратиться к геометрии, открытой современниками Ньютона. Соединим А и В хордой А ‾ В ‾. Вся хитрость состоит (как это часто делается для решения геометрических задач) в добавлении одной вспомогательной линии, в данном случае хорды А ‾ В ‾.

Рассмотрим теперь подобные треугольники на реальном рисунке и векторной диаграмме скоростей (фиг. 103). Радиусы ОА и ОВ на реальном рисунке образуют небольшой угол Е . Векторы скорости направлены по касательным перпендикулярно радиусам так, что вектор старой скорости v и вектор новой скорости v образуют тот же маленький угол Е [80] Если вы возьмете две линии, образующие угол X , и повернете каждую линию на 90°, то таким способом повернете все изображение на 90° и эти две линии в новом положении будут по-прежнему образовывать угол X . . Тогда на реальной картинке мы имеем треугольник ОАВ с равными сторонами R и R , образующими угол Е ; на векторной диаграмме имеется треугольник XYZ с равными сторонами v и v , образующими тот же угол Е . Поэтому треугольники ОАВ и XYZ подобны. Значит, должно иметь место следующее соотношение:

( Короткая сторона, Δ v / Одна из равных сторон, v ) = ( Короткая сторона, АВ / Одна из равных сторон, R )

в некотором треугольнике Δ v/ v = A‾ B‾/ R… в реальном треугольнике Δ v = v∙ A‾ B‾/ R

Теперь мы можем рассчитать «ускорение»:

УСКОРЕНИЕ = Δ v/Δ t= ( v∙ A‾ B‾/ R)/Δ t= ( v/ R)∙( A‾ B‾/Δ t)

Для дальнейшего нам необходимо установить, что такое A ‾ B ‾/Δ t .

Что представляет собой [( хорда A ‾ B ‾), деленная на ( время движения от А до B )]? Мы знаем, что такое дуга 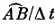. Это отношение ( расстояние )/( время ) на участке орбиты от А до B , т. е. скорость v . Но для очень короткой дуги, когда В близко к А , криволинейная дуга 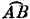очень близка к хорде A ‾ B ‾.

Посмотрите на серию картинок, показанных на фиг. 105.

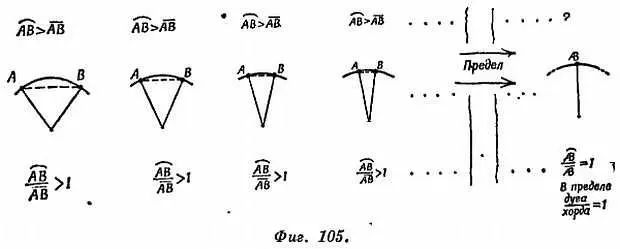
По мере сближения А и В дуга 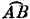и хорда A ‾ B ‾ становятся все меньше, в то же время уменьшается и различие между ними [81] Если вы не верите такому рассуждению и утверждаете, что расхождение между дугой и хордой остается неизменным и лишь маскируется сближением А и В , исследуйте следующий случай — фиг. 106: выберите размер АВ , затем перейдите к хорде аЬ , вдвое меньшей АВ , но увеличьте вдвое новый рисунок так, чтобы хорда аb стала равной выбранному вами размеру AВ . Теперь посмотрите на новую хорду а'Ь' . Ближе ли она к своей дуге? Заметим, что увеличение само по себе не изменяет относительных пропорций между хордой и ее дугой — оно не изменяет углы, а действует подобно увеличительному стеклу. . Говоря математическим языком, мы приближаемся к «пределу», когда В совпадает с А . Мы никогда не достигаем этого предела, но мы можем к нему приблизиться настолько, насколько захотим, и сделать различие между дугой и хордой настолько малым, насколько захотим.

Однако мы не только можем сделать разность 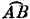— A ‾ B ‾ пренебрежимо малой — мы можем сделать пренебрежимо малым отношение (разность/хорда) или ( 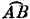— A ‾ B ‾)/ A ‾ B ‾. Это приводит к тому, что 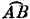/ A ‾ B ‾ становится очень близким к единице. Таким образом, мы можем сказать, что при большом расстоянии между А и В дуга немного больше хорды , при малом расстоянии дуга примерно равна хорде , а при еще меньшем расстоянии дуга почти равна хорде . При сколь угодно малом расстоянии в пределе дуга равна хорде . Математики предпочитают описывать этот предел так: LIm(дуга/хорда) = 1. Теперь мы хотим определить ускорение в некоторый момент времени , когда В и А практически совпадают. Мы не собираемся определять значение этой величины, усредненное по большому расстоянию. Мы хотим знать предел ускорения, когда В совпадает с А . Таким образом, мы говорим: дуга = хорда, 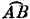— A ‾ B ‾. Тогда