Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Дуга/Δ t= Хорда/Δ t, или 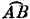/Δ t = A‾ B‾/Δ tв пределе.

Следовательно,

Ускорение= Δ v/Δ t= ( v/ R)∙ A‾ B‾/Δ t= ( v/ R)∙( v), в пределе ( v/ R)∙ 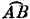/Δ t

так как 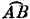/Δ t есть v . Тогда ускорение Δ v/Δ t= ( v/ R)∙( v) или v 2/ R

или ( Скорость на орбите) 2/( Радиус орбиты)

Это соотношение ускорение — v 2/ R очень важно. Мы будем использовать его в теории движения планет, при изучении движения электронов, при изготовлении масс-спектрографов и конструировании циклотронов — везде, где мы сталкиваемся с движением по орбите. Было бы очень важно повторить для себя вывод этого соотношения и поверить в его значение. Поняв, как это делается, вы можете сократить вывод, ограничившись коротким объяснением, двумя эскизами и несколькими алгебраическими выражениями.

Два важных вопроса

Полученный нами результат, ускорение= v 2/ R, вызывает два вопроса:

1. Каким образом может движущееся тело иметь ускорение, но не двигаться быстрее или же не перемещаться к центру круга?

2. Не нужна ли сила для ускорения тела в направлении его движения в соответствии с соотношением F= M∙ a. He действует t ли на массу М , движущуюся по окружности, сила М∙ v 2/ R .

Оба эти вопроса являются выражением тех, реальных трудностей, которые возникли сразу же, как только люди оказались перед необходимостью объяснить движение планет по орбитам. Ответ на вопрос 2 следует из эксперимента: «Да, каждое реальное движение по окружности требует наличия реальной силы, направленной внутрь, a М∙ v 2/ R есть величина этой силы». Чтобы тело могло двигаться по окружности, на него должна действовать сила, направленная к центру. Такая сила может осуществляться с помощью какого-либо реального внешнего воздействия — веревки, пружины или силы тяготения [82] Люди иногда думают, что движение по окружности создает направленную вовнутрь силу, необходимую для поддержания его. Ребенок, который хочет получить леденец, не думает, что от его желания появятся деньги на покупку леденца. Какой-то внешний агент в образе доброго дяди может обеспечить деньги для этой покупки, иначе леденца не будет. Условие движения по окружности аналогично по смыслу. Реальное внешнее воздействие должно обеспечить надлежащую силу, иначе не получится круговой орбиты. .

Пример А

Вращайте камень, привязанный к веревке (фиг. 107). Вы тянете за веревку, а веревка тянет камень к центру. Веревка буксирует камень и сообщает ему некоторое количество движения в новом направлении.

Представим себе, что веревка делает серию слабых рывков; рывок — и скорость изменила свое направление, еще рывок — снова изменение, еще, еще и так вдоль всей окружности. Если вы отпустите веревку, рывки прекратятся, прекратится и изменение скорости, а камень будет продолжать двигаться по касательной. (Сказать, что «камень улетает по касательной» — значит ввести в заблуждение).

Вращение камня на веревке по окружности, расположенной в горизонтальной плоскости, под действием пружины или веса обеспечивает наличие внутренней силы, которую можно измерить. Ниже описаны 3 опыта. Любой из них можно использовать для проверки справедливости соотношения F= M∙ v 2/ R.

Фиг. 107. Вращение камня на веревке.

Опыт 1.Металлический шар, связанный шнуром со стальной пружиной, равномерно вращается по кругу (фиг. 108).

Пружина растягивается до некоторых пор, а затем длина R шнура + пружины остается постоянной во время вращения. Движение хронометрируется и затем рассчитывается величина силы М∙ v 2/ R , направленной внутрь. Эта сила, фактически действующая со стороны пружины, определяется в отдельном эксперименте путем навешивания нагрузки на пружину.

Чтобы увидеть, насколько растянулась пружина при вращении, необходимо некоторое устройство.

Опыт 2.Металлический шар, привязанный к шнуру, равномерно вращается по кругу (фиг. 109).

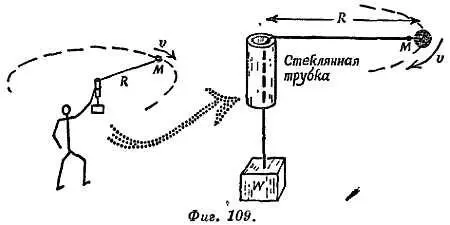
Шнур спускается вниз в стеклянной трубке с гладкими открытыми концами и оттягивается с помощью груза W . Двигая трубку по маленькому кругу, экспериментатор поддерживает движение шара по горизонтальному кругу. Движение хронометрируется, и определяется значение силы М∙ v 2/ R , направленной внутрь. Эта сила, фактически действующая на шар со стороны шнура, является силой натяжения и практически равна (за вычетом незначительного трения) весу груза W .

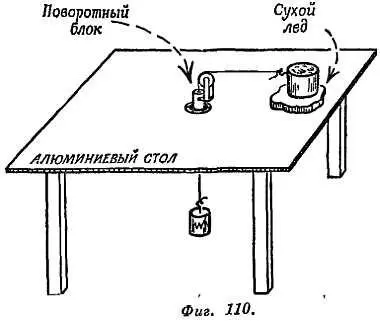
Опыт 3.В этом варианте опыта 2 , когда трения нет, шар заменен тяжелым блоком, расположенным на куске сухого льда, скользящем по алюминиевому столу (фиг. 110). Шнур пропущен через отверстие в центре стола, а стеклянная трубка заменена маленьким блоком, который поворачивается в этом отверстии на очень хороших подшипниках.

Пример Б

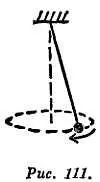
Проследите за движением «конического маятника» (фиг. 111). Гиря маятника, движущаяся по окружности в горизонтальной плоскости, подвергается воздействию двух реальных сил — веса и натяжения веревки. Если вы измерите эти силы и сложите их как векторы, вы можете найти результирующую горизонтальную силу, направленную внутрь к центру орбиты гири. Измерив параметры орбиты и время одного оборота, вы можете проверить соотношение а= v 2/ R

Пример В

Шарик катится внутри воронка

по эллиптической орбите (фиг. 112, а ).

Пример Г

Стальной шар катится по горизонтально расположенной стеклянной пластине в магнитном поле (фиг. 112, б ). На практике обычно используется электромагнит, который располагается под столом. (Магнитное поле намагничивает шар так, что он притягивается к полюсу магнита. Получая подходящее ускорение, этот шар будет кататься вокруг полюса магнита.)

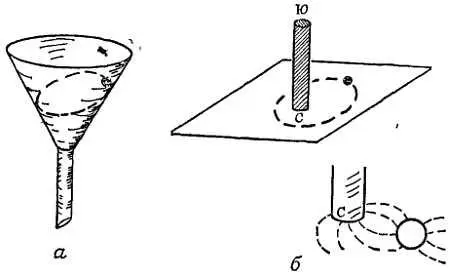
Фиг. 112. Примеры кругового движения с центростремительной силой.