Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Задача 4

Из геометрии следует, что точка (или небольшое тело), движущаяся в постоянной скоростью v no кругу радиусом R , имеет центростремительное ускорение v 2/ R . Напишите геометрический вывод этого выражения. (Вы можете предположить, что скорость и ускорение — векторы, т. е. подчиняются законам геометрического сложения и вычитания. Вы можете пользоваться свойствами подобных треугольников. Дайте большие, очень четкие эскизы: один — для фактической картины, другой — для векторов.)

Задача 5

В предлагаемых ниже вопросах предполагается: 1) центростремительное ускорение равно v 2/ R и 2) в случае этого движения F = M ∙ a . (Вспомним, что всякий раз, когда вводится F = M ∙ a , сила должна быть выражена в ньютонах, если масса выражена в килограммах.)

а) Камень массой 2,00 кг вращается (с помощью веревки) по горизонтальной поверхности стола без трения. Длина веревки 4,0 м, следовательно, круг имеет радиус, равный 4 м. Камень движется по орбите со скоростью 7,00 м/сек. Рассчитайте ускорение камня, натяжение веревки. Приведите краткие пояснения.

б) Предположим, что веревка разрывается как pas при том натяжении, которое ей определили выше. Какова будет разрывающая сила в килограммах силы, кГ?

в) Как и в вопросе ( а ), камень массой 2,00 кг вращается по кругу на веревке длиной 4,0 м, но с такой скоростью, что он совершает пять оборотов ее 2 сек.

Рассчитайте его скорость (ответ оставьте в виде сомножителей, не подставляя численного значения π ).

Рассчитайте натяжение каната. (Укажите единица измерения в ответе. Можно положить π 2= 10.)

Задача 6

Веревка, подвешенная вертикально, может выдержать только 10,0 кг и рвется при малейшем увеличении нагрузки.

а) Какова разрушающая сила в килограммах силы?

б) Какова эта разрушающая сила в ньютонах?

Кусок такой веревки длиной 1,00 м используется для вращения камня массой 2,0 кг по горизонтальному кругу все быстрее и быстрее, пока веревка не разорвется.

в) Рассчитайте максимальную скорость камня на орбите и приведите краткое объяснение, как вы выполнили этот расчет.

Фиг. 145. К задаче 6.

Задача 7

Игрок с ракеткой, на которой находится мяч, крутит ракеткой перед собой. Объясните, каким образом такое движение не позволяет мячу упасть.

Фиг. 146. К задаче 7.

Задача 8

Самолет, летящий со скоростью 600 фут/сек (410 миль в час), преследует маленький самолет, летящий со скоростью 300 фут/сек. Маленький самолет поворачивает и удаляется по горизонтальному полукругу; самолет-преследователь старается нагнать его. Пилот может выдержать ускорение только до 5 g .

а) Рассчитайте радиус наименьшего полукруга, который пилот маленького самолета может благополучно выполнить при скорости 300 фут/сек.

б) Как долго (примерно) будет двигаться по своему полукругу маленький самолет?

в) Вычислите радиус наименьшего полукруга, безопасного для самолета-преследователя,

г) Где будет находиться самолет-преследователь, когда маленький самолет уже закончит свой полукруг (обозначьте его путь на эскизе)?

Задача 9. Вариант вывода соотношения а = v 2/R (метод Ньютона)

Если тело движется по окружности от А до В , рассмотрите его как падающее тело с постоянным ускорением, направленным вниз. За время t оно пролетит с ускорением а расстояние h от той точки, в которой оно раньше покоилось.

а) Напишите уравнение для а через h и t , предполагая, что а постоянно.

б) Используя геометрическое свойство хорд круга, напишите уравнение, в котором h было бы выражено через другие измеряемые величины, приведенные на диаграмме.

в) Подставьте выражение для h в уравнение, полученное в вопросе ( а ).

г) Представьте, что В движется все ближе и ближе к А . Если В —> А , то горизонтальное расстояние х —> к дуге 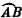и, поскольку В —> А , хорда MN —> к диаметру 2 R . Внесите эти изменения в выражение для ускорения.

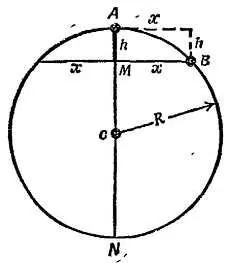
Фиг. 147. К задаче 9.

Задача 10. Центрифугирование

а) Центрифуга вращает пробирку по кругу со средним радиусом 1 фут со скоростью 5000 оборотов в минуту; содержимое пробирки находится при этом в силовом поле, во много раз большем g . Во сколько раз большем g ?

б) Образец мутной воды содержит частицы, размер которых примерно равен размерам, кровяных шариков (диаметр 10 -5м). Если пробирка расположена вертикально, частицы падают на дно с постоянной скоростью ~ 1/ 4дм/мин. Таким образом, объем жидкости высотой 4 дм полностью очистится примерно зa 1/ 4часа. (Эти частицы не осядут все на дно. Диффузия, связанная, с броуновским движением, поддерживает некоторое их количество во взвешенном состоянии.) За какое время тот же образец станет прозрачным в центрифуге, обеспечивающей ускорение, определенное в вопросе ( а )?

в) Белковые молекулы [диаметр которых в несколько сотен раз меньше диаметра частичек мути, о которых говорится в вопросе ( б ), но велик по сравнению с диаметром других молекул, скажем соли или воздуха] осаждаются в воде примерно в 300 000 раз медленнее, чем частички мути (вопрос б ). За какое время станет прозрачной помещенная в центрифугу 4-дюймовая пробирка, содержащая суспензию таких белковых молекул в воде?

г) Если, эту белковую суспензию не помещать в центрифугу, она никогда не станет прозрачной. Почему?

д) Если известна плотность частиц, то, исходя из спорости прояснения жидкости, можно определить диаметры частиц. (Сила торможения маленькой сферы пропорциональна ее радиусу и скорости.) Частички грязи (вопрос б ) могут быть измерены с помощью микроскопа, молекулы же белка увидеть невозможно. «Химические» измерения (осмотическое давление) показывают, что молекулы белка в 10 6раз тяжелее атома водорода. Какая важная информация о строении атома может быть получена с помощью измерений на центрифуге?

Жизнь и труды Ньютона