Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Фиг. 10. Изображение ошибки на графиках.

Физики часто приводят ошибки или погрешности на графиках, но объединяют их и выражают погрешности величин, откладываемых на графике по горизонтали и по вертикали, в виде погрешности величины, откладываемой по вертикали. Экспериментатор оценивает вероятную ошибку Δy , допущенную им при измерении величины, откладываемой по вертикали. Он оценивает также вероятную ошибку Δх ; величины, откладываемой по горизонтали, а затем задает вопрос: «Если я допустил такую ошибку Δх , то как велика при этом будет ошибка величины у , которая бы в точности ее учитывала?». Это дает ему значение Δy °, эквивалентное допущенной им ошибке Δх . Он проводит вертикальную прямую длиной ( Δy + Δy °) с центром в экспериментальной точке. Тогда каждой точке, наносимой на график, будет соответствовать такое пятно, выражающее величину погрешности, как показано на фиг. 10, в .

Нахождение скорости при помощи касательных

Если бы мы могли построить график изменения скорости со временем, то это позволило бы непосредственно изучать ускорение.

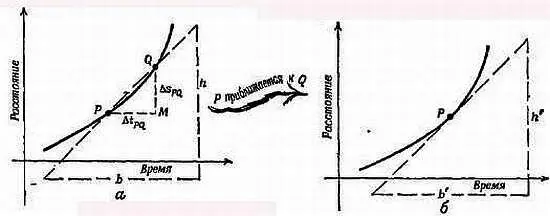
Фиг. 11. Скорость равна наклону касательной.

Для этого необходимо оценить значение скорости в различные моменты времени.

Мы можем определить скорость, проводя касательные к кривой, описывающей зависимость пройденного расстояния от времени. Если провести касательную к кривой в некоторой точке, то наклон касательной даст скорость тела в данный момент времени и в данном месте. Чтобы убедиться в этом, выберем некоторую точку Р на этой кривой (фиг. 11), а затем переместимся вверх по кривой в точку Q , соответствующую более позднему моменту времени. Находясь в точке Р , тело уже прошло некоторое расстояние за какой-то промежуток времени. От Р до Q тело проходит еще небольшой отрезок пути Δs за малый промежуток времени Δt .

Тогда средняя скорость в интервале между Р и Q равна отношению

[РАССТОЯНИЕ, ПРОЙДЕННОЕ ОТ РДО Q]/[ВРЕМЯ ПЕРЕМЕЩЕНИЯ ОТ РДО Q]

или

СРЕДНЯЯ СКОРОСТЬ = Δ s PQ/Δ t PQ(см. фиг. 11, a ),

= ВЫСОТА/ОСНОВАНИЕ МАЛОГО ТРЕУГОЛЬНИКА PQM ,

= ВЫСОТА/ОСНОВАНИЕ ЛЮБОГО ТРЕУГОЛЬНИКА больших размеров, подобного треугольнику PQM ,

= h/ bна фиг. 11, а ,

= наклон хорды, соединяющей точки Р и Q , или

ВЫСОТА/ОСНОВАНИЕ.

Если точки Р и Q расположены очень близко одна от другой, то соединяющая их линия почти совпадает с касательной к кривой в «точке» PQ , и скорость по-прежнему определяется наклоном этой «касательной». В пределе, как говорят в математике, когда точка Р приближается к Q , хорда превращается в касательную к кривой в этой точке; величины Δs и Δt становятся равными нулю, но отношение Δs / dt по-прежнему имеет вполне определенное значение, равное отношению h '/ b ' в любом треугольнике больших размеров, у которого касательная является гипотенузой, как на фиг. 11, б . Если PQ — хорда, то ее наклон определяет среднюю скорость движения от точки Р к точке Q. В пределе, когда Р и Q совпадают, наклон касательной определяет скорость в момент времени, соответствующий точке Р , в которой проводится касательная. Дело в том, что наклон касательной совпадает с наклоном бесконечно короткого отрезка кривой, характеризующего движение в данной точке. Проводя касательные во многих точках кривой и измеряя наклон этих касательных, мы могли бы определить несколько значений скорости, по которым можно было бы построить новый график, выражающий зависимость скорости от времени .

Форма этого графика позволила бы нам судить о том, постоянно ли ускорение, однако проведение касательных — дело не простое, и, чтобы с уверенностью делать выводы, пользуясь полученным набором значений наклона касательных, пришлось бы строить исходный график очень тщательно, с большим числом дополнительных точек. Поэтому на практике постоянство ускорения проверяют путем построения другого графика, выражающего зависимость расстояния от квадрата времени .

Однако мы можем воспользоваться указанным выше свойством касательной для построения первоначального графика. Хотя наш график, представленный на фиг. 8, проходит через начало координат, трудно судить о ходе кривой вблизи начала координат , поскольку измерять очень короткие перемещения сложно. Мы не можем с уверенностью сказать, какая из трех представленных на фиг. 12 кривых верна.

Фиг. 12. Различные варианты графика фиг. 8, изображающего зависимость пройденного расстояния от времени.

Мы можем выяснить это, рассуждая следующим образом: согласно полученным данным, тело начало двигаться из состояния покоя. Следовательно, начальная скорость тела равна нулю. Поэтому наклон касательной к кривой в начале координат должен быть равен нулю, касательная должна быть расположена горизонтально. Отсюда можно заключить, что из трех кривых фиг. 12 верна, по-видимому, средняя.

Арифметическая проверка постоянства ускорения

Результаты нашего мысленного опыта можно еще проверить с помощью арифметического расчета. Если ускорение постоянно, то

РАССТОЯНИЕ = (ПОСТОЯННАЯ)∙(ВРЕМЯ) 2.

Поэтому расстояние/(время) 2 = const . И наоборот, если отношение ( расстояние)/(время) 2постоянно, то постоянно и ускорение. Чтобы проверить это, расширим нашу таблицу, дополнив ее еще одним столбцом (табл. 4).

Чтобы из чисел, приведенных в последнем столбце, сделать определенный вывод, необходимо знать точность измерений. Иначе мы сможем лишь сказать, что движение, по-видимому, происходит с ускорением, довольно близким к постоянному.

Как графический, так и арифметический способы проверки, о которых только что шла речь, трудно применить при малом количестве данных. Но это всего лишь мысленный пример: истинная проверка должна явиться результатом ваших собственных опытов .

Труды многих ученых специалистов и тех, кто просто интересуется физикой, утвердили веру в открытие Галилея: тела, свободно падающие под действием земного тяготения, и тела, скользящие или скатывающиеся вниз по наклонной плоскости под действием с1, илы тяжести, движутся с постоянным ускорением.

Дальнейшие эксперименты показывают, что ускорение имеет одно и то же значение даже в том случае, если тело начинает, движение не из состояния покоя, а получив толчок. Если в момент пуска часов тело имеет скорость v 0, то соотношение s = 1/ 2 at 2уже неверно; мы должны воспользоваться в этом случае соотношением s = v 0+ 1/ 2 at 2(см. приложение I ). Однако ускорение а остается тем же самым. Едва ли оно могло бы быть другим: каким образом шар может «узнать», что он начал двигаться после полученного толчка, а не скатывался с большей высоты по той же самой наклонной плоскости?