Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

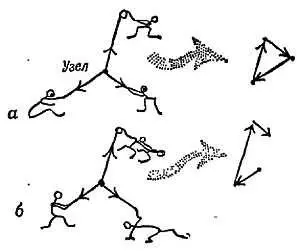
Фиг. 68. Три силы.

а— три силы в равновесии; б— три силы не находятся в равновесии.

Рассмотрим теперь несколько примеров решения инженерных задач на сложение и разложение сил (задач статики). После того как вы разберете их вместе с нами, попытайтесь решить задачи, приведенные в конце главы.

Задача 1

Три мальчика тянут в разных направлениях в горизонтальной плоскости веревки, прикрепленные к большому железному кольцу (фиг. 69). Предположим, что на кольцо не действуют другие силы, даже сила тяжести. Каждый мальчик тянет веревку с силой 10 кГ, и кольцо остается в покое.

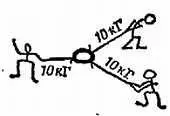
Фиг. 69. К задаче 1.

а) Чему равна величина суммы, тянущих сил?

б) Начертите векторную диаграмму сил, сложив эти силы.

в) Изобразите схему опыта, какой она выглядит сверху, и покажите направления действующих на кольцо сил.

г) Представьте себе, что один из мальчиков внезапно выпускает веревку из рук, а другие продолжают тянуть свои веревки. Каковы величина и направление суммы, сил, развиваемых двумя оставшимися мальчиками?

Пример А

Тяжелый маятник состоит из груза весом 4 кГ, подвешенного на веревке длиной 5 м, (фиг. 70). Груз оттягивается в сторону другой веревкой, посредством которой к грузу маятника прикладывают горизонтальную силу 3 кГ.

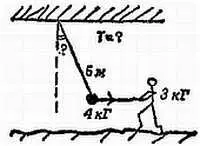
Фиг. 70. Общая схема, иллюстрирующая формулировку примера А.

1) Рассчитайте натяжение веревки маятника.

2) Какой угол образует маятник с вертикалью?

На груз маятника действуют три силы:

а) вес груза 4 кГ, направленный вертикально вниз;

б) горизонтальная сила натяжения 3 кГ;

в) натяжение веревки маятника неизвестной величины, направленное вдоль веревки вверх.

Чтобы рассчитать натяжение веревки маятника, построим две диаграммы; их нужно строить отдельно, ибо они относятся к совершенно разным вещам. Реальная схема — это рисунок, изображающий конструкцию, с которой мы имеем дело.

Эту схему можно изобразить в масштабе или просто нарисовать рисунок и указать на нем размеры. Диаграмма сил — это векторная диаграмма, на которой силы изображаются отрезками прямых. Диаграмму сил не следует строить над реальной схемой, хотя обе они могут быть сходны . В этой задаче мы будем строить векторную диаграмму для трех сил, действующих на груз маятника. После того как груз перестает раскачиваться и приходит в состояние покоя, сумма этих сил должна быть равна нулю. Поэтому векторы сил, построенные в масштабе, должны образовать замкнутый треугольник (фиг. 71).

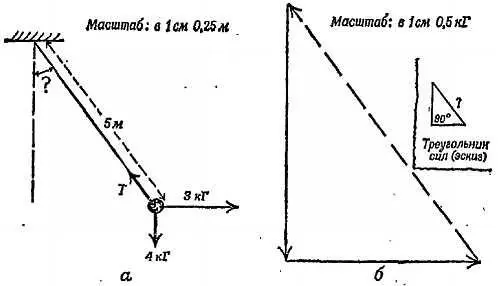
Фиг. 71. Схема приложения сил ( а) и диаграмма сил для груза ( б).

Единственный известный размер показан в масштабе, угол может быть изображен неверно.

Прежде всего проводим вектор, о котором нам все известно, — вектор силы, действующей на груз маятника по вертикали и равной весу груза 4 кГ. Изобразим этот вектор вертикальным отрезком АВ длиной 4 см со стрелкой, направленной вниз [37] Точки А, В, С не показаны на фиг. 71, б . Проставьте их. .

Затем мы добавляем еще один вектор, о котором нам опять-таки все известно, — горизонтальную силу 3 кГ, изображаемую отрезком ВС длиной 3 см. Отрезок, изображающий третью силу, должен замыкать треугольник, поскольку сумма сил равна нулю. Поэтому третья сила должна изображаться отрезком СА .

Измерив эту сторону построенного треугольника, мы находим 5 см, что соответствует натяжению веревки маятника 5 кГ.

Мы могли бы в этом случае постудить и по-другому: набросать примерный рисунок и, воспользовавшись теоремой Пифагора, найти искомую длину третьей стороны треугольника, она равна √(4 2+ 3 2), или √25, т. е. 5 см. Направление этой стороны треугольника образует с вертикалью угол, характеризующийся уклоном (тангенсом), равным 3/ 4. По таблицам тригонометрических функций или путем деления находим, что этот угол примерно равен 37°. Переходя к реальному маятнику, мы можем теперь сказать, что натяжение веревки равно 5 кГ и что веревка образует с вертикалью угол 37°.

Пример Б

Груз маятника 5 кГ, подвешенный на веревке длиной 1,5 м, оттянут в сторону на 0,9 м горизонтальной силой F . Какова величина этой силы? На фиг. 72 показан схематический рисунок и этапы построения диаграммы сил.

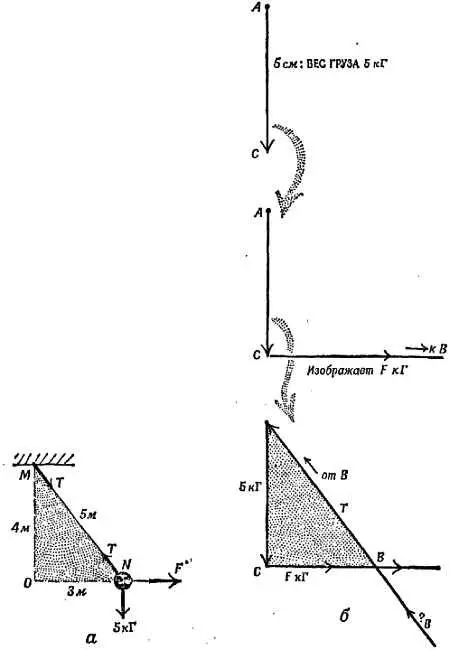
Фиг. 72. Построение диаграммы сил.

а— схема приложения сил; б— этапы построения диаграммы сил; поскольку треугольник может быть задан двумя углами и одной из сторон, построить диаграмму сил возможно.

Построение диаграммы сил мы начинаем, проведя АС , вектор единственной силы, о которой нам все известно, — силы, направленной вниз и равной весу груза 5 кГ. Теперь прибавим к ней горизонтальную силу, т. е. проведем горизонтальную прямую из конца вектора АС . Но величина этой силы нам пока неизвестна, поэтому мы не знаем, какой длины должен быть изображающий ее отрезок. Однако мы знаем, что, прибавив к остальным двум силам натяжение веревки маятника, мы должны получить замкнутый треугольник сил (если груз маятника находится в равновесии). Поэтому вектор силы натяжения должен выходить из конца силы F и оканчиваться в точке А . Кроме того, натяжение веревки должно быть направлено вдоль самой веревки. (Можете ли вы представить себе веревку, позволяющую тянуть в каком-то ином направлении, нежели вдоль самой веревки?) Таким образом, мы переносим направление веревки с рисунка, изображающего реальную схему, на диаграмму сил и проводим через точку А прямую, параллельную направлению веревки. Этот отрезок наклонной прямой образует третью сторону треугольника сил ВА — натяжение веревки. Угол В примыкает к прямой, проходящей наклонно, и к горизонтальной прямой, при этом он должен быть образован пересечением обеих этих прямых. Найдя положение точки В , мы узнаем величину силы F , попутно мы определили также натяжение веревки маятника. Для нахождения величины интересующей нас силы мы построили точный чертеж и произвели измерение.

В этом случае числовые данные позволяют проделать простые вычисления, исходя из геометрических соображений, и можно рассчитать F по приближенным рисункам, рассуждая следующим образом: стороны треугольника сил ABC параллельны сторонам треугольника MNО на реальной схеме, следовательно [38] Если вам еще неизвестны свойства подобных треугольников, обратитесь к какому-нибудь учебнику геометрии или попросите, чтобы вам их объяснили: необходимо уметь уверенно ими пользоваться. , эти треугольники подобны. (По теореме Пифагора находим ОМ = 1,2 м.)