Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

x= v гор tи y= 1/ 2 gt 2

Следовательно,

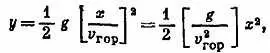
т. е. у= (постоянная) x 2, поскольку 1/ 2 g/ v 2 гop— постоянная величина.

Это уравнение параболы [34] Прежде парабола определялась как одна из кривых, получающихся при сечении конуса плоскостью. Сейчас параболу часто определяют как кривую, описываемую уравнением y = (постоянная)∙ х 2 , или у ~ x 2 . В одном из разделов аналитической геометрии показывается, что алгебраическое и геометрическое определения эквивалентны.

Воспользовавшись подобным уравнением, можно построить на клетчатой бумаге превосходные графики параболы. Постройте на бумаге с сантиметровыми клетками кривую, описываемую уравнением y = 1/ 2 x 2, взяв х = — 4, —3, —2, —1, 0, 1, 2 см и т. д.

Попытайтесь подогнать траекторию движения реального тела к этой кривой. Положите лист бумаги, на котором построена кривая, на чертежную доску, расположенную наклонно к плоскости стола, и скатывайте по ней шарик или держите лист бумаги отвесно и подбрасывайте перед ним какой-нибудь небольшой предмет.

Движение снаряда, выпущенного из пушки под углом к горизонту

Если снаряд выпущен не горизонтально, а вверх, под некоторым углом к горизонту, то его траектория по-прежнему будет параболой. Алгебраически это можно показать, используя уравнение s= v 0 t+ 1/ 2 gt 2,a не s= 1/ 2 gt 2. Таким образом, мы воспользуемся очевидной симметрией криволинейной траектории движения и можем сказать, что замедленное движение тела вверх до вершины траектории должно совпадать с ускоренным движением вниз, начинающимся от вершины, поэтому можно начертить всю траекторию, исходя из рассмотренной задачи движения снаряда, выпущенного горизонтально. Но все это лишь разумное предположение, хотя эксперимент подтверждает его. Можно рассуждать еще и так: двигаясь по ниспадающему участку траектории от вершины О , камень не может «знать», началось ли его движение в точке О или раньше, или позже. Поэтому камень, брошенный в какой-либо точке этого участка траектории, скажем в точке А , в сторону и вниз, должен двигаться по той же траектории, что и камень, брошенный горизонтально из вершины О , лежащей выше (фиг. 59).

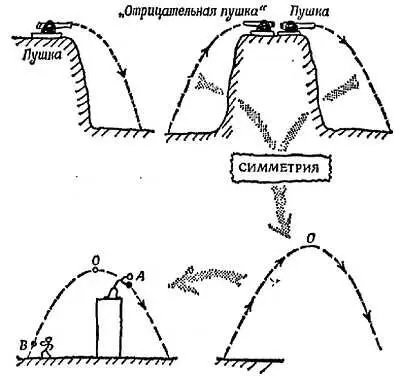
Фиг. 59. Движение тела вверх и вниз.

Симметрия траектории заставляет предполагать, что движение вверх до «отрицательной пушки» подобно движению вниз от «нормальной» пушки, стоящей на той же горе. Вместе эти движения дают полную параболу. В таком случае тело, начавшее движение по этой параболе из точки А , должно двигаться по той же траектории, как если бы движение его началось раньше из вершины О. Соображения симметрии позволяют распространить эти рассуждения на всю параболу.

То же самое справедливо для камня, брошенного вверх в точке В , Это наводит на мысль о расширении представления о независимости движений. Вертикальная компонента начального движения также остается неизменной, хотя к ней добавляется ускоренное движение свободного падения. С этим вертикальным движением, происходящим с постоянной скоростью, связано расстояние v 0 t в соотношении s= v 0 t+ 1/ 2 gt 2. Тогда можно объединить оба постоянных движения, вертикальную и горизонтальную компоненты начального броска, и сказать, что начальное движение тела, брошенного под узлом к горизонту, остается неизменным во время полета , хотя к нему добавляется движение свободного падения по вертикали, которое обусловливает появление в уравнении слагаемого 1/ 2 gt 2. Итак, можно считать, что камень, брошенный, как показано на фиг. 60, совершает два движения: начальное движение вдоль прямой 45 и свободное падение, в котором камень проходит расстояния, отсчитанные от точек на прямой АВ , взятых через последовательные равные промежутки.

Фиг. 60. Анализ движения тела.

Это можно показать с помощью опыта с обезьянкой и ружьем.

Представим себе, что охотник, не принимающий во внимание силы земного тяготения, целится в обезьянку, которая повисла на дереве, ухватившись одной лапой за ветку. При выстреле пуля не попадет в обезьянку из-за свободного падения, как показано на фиг. 61.

Фиг. 61. Опыт с обезьянкой и воздушным ружьем.

Когда пуля вылетает из ружья, она разрывает контакт, электромагнит выключается и отпускает «обезьянку».

Предположим теперь, что обезьянка следит за действиями охотника и, заметив вспышку, выпускает ветку в тот момент, когда пуля вылетает из ружья. С этого момента и обезьянка и пуля совершают ускоренные движения вниз под действием силы тяжести; обезьянка падает из состояния покоя, пуля, согласно нашему последнему представлению, падает от своей «невозмущенной траектории», прямой АВ . Что же происходит? Это можно показать при помощи железной фигурки обезьянки, которую удерживает электромагнит, обесточиваемый разрывом цепи при вылете пули из ствола воздушного ружья, направленного на фигурку.

Такие эксперименты подтверждают наше предположение о том, что падение по вертикали совершенно не зависит от начального движения, которое неизменно. Любое летящее тело с начала движения совершает свободное падение. Оно проходит 0.3, 1.4, 3.6, 4.9 и т. д. метров за 1, 2, 3, 4… четвертьсекундных промежутка времени после начала движения. Если линия начального движения направлена под углом к горизонту, то тело сначала поднимается вверх, а потом падает, тогда расстояние, проходимое им в единицу времени в свободном падении, станет больше того расстояния, на которое тело поднимается вверх за каждую единицу, времени вследствие сообщенного ему начального движения. (Обратите внимание, что показанная на фиг. 62 траектория является параболой.)

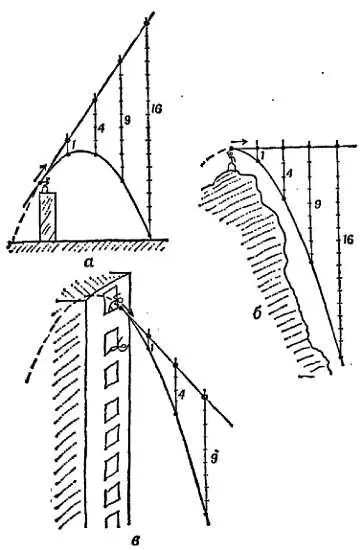
Фиг. 62. Свободное падение тела.

Вы видите, как мы своими рассуждениями разделили задачу о движении летящего снаряда на части, облегчив ее решение и подготовив для дальнейшего изучения специалистами по баллистике.

Наши усилия не внесли новых сведений, но облегчили пользование уже известными сведениями.

Когда движущимися телами являются быстрые электроны (или заряженные атомы) и на них воздействуют не силы тяготения, а электрические и магнитные поля, то к ним применимы такие же «правила», и мы используем изменения траектории для получения информации об электрическом заряде, массе и скорости электрона. Потом мы считаем, что поведение движущихся тел подчиняется тем же правилам, и предсказываем воздействие полей на частицы, движущиеся с другими скоростями. Так поступают инженеры — специалисты по электронным приборам при проектировании телевизионных трубок и других радиоэлектронных устройств; такие же расчеты проделывают ученые-атомники, когда искривляют пучки электронов или атомов, бомбардируя ими мишени или опознавая тяжелые и легкие атомы по различиям в их траекториях.