Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

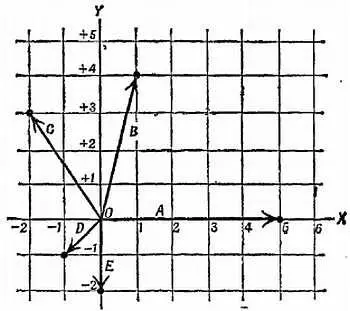
Фиг. 51.К задаче 10.

Проведите отрезок, выражающий сумму. Измерьте и запишите его величину. Чтобы определить направление суммы, нужно либо измерить какой-то угол, либо найти наклон отрезка, выражающего сумму. Испробуйте оба способа следующим образом:

а) Измерьте и запишите угол между суммой и самым первым вектором А .

б) Проведите две взаимно перпендикулярные оси ОХ и ОY , направив ось ОХ вдоль вектора А . Затем опустите перпендикуляр h из конца векторной суммы на ось ОХ (точно проводить этот перпендикуляр не нужно, можно просто измерить его длину). Измерьте высоту h и длину основания Ь , отсекаемого перпендикуляром на оси ОХ . После этого вычислите отношение (высота h )/(основание b ), которое называется наклоном отрезка R . Это позволит нам задать В , как вектор, величина которого равна…? а направление имеет наклон…?

Задача 11. Сумма однозначна

Получится ли иная векторная сумма, если складывать векторы в другой порядке? Проделайте снова задачу 10 на листе миллиметровки; начните, как и раньше, с вектора А , но прибавляйте к нему остальные векторы в другой последовательности: В, Е, D, С . Определите величину и направление суммы в этом случае.

Задача 12. Некоторые соображения по поводу сложения векторов

Представим себе векторы А, В, С, D, E в задаче 10 как перемещений, которые корабль должен совершить одно за другим. Представим себе оси ОХ, OY как направления восток и север, определяемые по компасу. Тогда одно перемещение, скажем В , переносит нас на некоторое расстояние к северу и на некоторое расстояние к востоку. Мы можем сказать, что перемещение В изменяет наш курс на столько-тo к северу и на столько-то к востоку. Фактически, же мы представляем себе перемещение В расчлененным, на компоненты, северную и восточную. Это называется «разложением вектора В на северную и восточную компоненты.

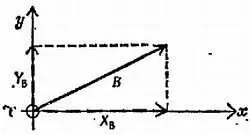
Фиг. 52. К задаче 12.

Разложение вектора на пару взаимно перпендикулярных «компонент» XB и YB, заменяющих этот вектор

Мы можем таким же образом разложить все векторы. Некоторые из восточных или северных компонент могут оказаться отрицательными. Сумму R тоже можно представить себе разложенной на восточную и северную компоненты. Когда мы складываем векторы, А, В …, то каждый из них вносит свою долю в изменение курса к востоку и к северу.

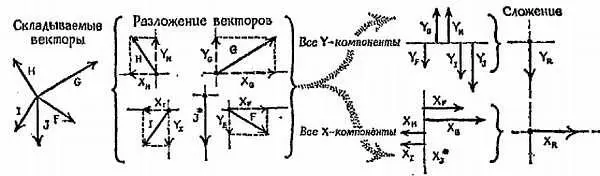
Фиг. 53. К задаче 12.

Разложение векторов F, G, H, I, Jна компоненты (составляющие) вдоль направлений X(восточное) и Y(северное).

а) Как, по-вашему, связана восточная компонента суммы с восточными компонентами векторов А, В ,?

б) А как связана северная компонента суммы?

в) Как вы думаете, изменятся ли ответы на вопросы, ( а ) и ( б ), если изменить порядок сложения отдельных векторов?

Задача 13. Еще один способ сложения векторов

Предыдущая задача указывает еще на один способ сложения векторов, очень удобный при большом числе складываемых векторов, особенно если заданы углы, и мы умеем пользоваться тригонометрией. Мы едва ли будем пользоваться тригонометрией в нашем курсе, и элементы ее приводятся лишь, чтобы, показать, что существует стройный метод.

а) предположим, что известны, восточная компонента Х Rсуммы R и северная компонента Y R. Ha фиг.54 показаны R, Х R и Y R. Каким образом можно вычислить величину R , зная Х R и Y R? Запищите, уравнение.

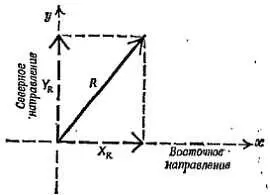
Фиг. 54. К задаче 13.

б) Предположим, что известны восточная и северная компоненты каждого из векторов А, В …. (Предположим, что вектор А разлагается на компоненты Х А, Y Аи точно так же разлагаются остальные векторы.) Как бы вы вычислили восточную и северную компоненту R ? Напишите уравнения для Х Rи Y R. ( Примечание . Математики часто пользуются знаком Σ, заглавной греческой буквой «сигма», для обозначения «суммы всех величин). Например, если у членов банды А, В, С и др. имеются наличными М Адолларов, M Вдолларов и т. д., то общее количество наличных денег у банды равно М Адолларов + M В+ М С+… и это записывается в виде Σ М . Воспользуйтесь знаком Σ при решении этой задачи.)

в) Запишите указания для вычисления величины суммы R нескольких векторов, если заданы восточная и северная компоненты всех векторов.

г) Дайте такие указания применительно к векторам задачи 10. Перерисуйте векторы задачи 10 на новом листе миллиметровки. Проведите необходимые перпендикуляры и измерьте восточную и северную компоненты (припишите знаки минус всем компонентам, направленным на запад или юг).

Вычислите величину суммы векторов. Вычислите наклон этой суммы, используя вектор А как горизонтальную базовую линию.

Задача 14(для тех, кто знаком с тригонометрией)

В задаче 10 векторы А, В, С, D, Е образуют следующие углы с вектором А , который, как принято, направлен на восток: А: 0°; В : 76°,0; С : 123°,7; D : 225°,0; Е : 270°,0. Длины векторов, если чертеж сделан на миллиметровке с сантиметровыми клетками, равны приблизительно; А : 8,00; В : 4,12; С : 3,61; D : 1,41; Е : 2,00 см. Воспользуйтесь правилами тригонометрии и найдите северную и восточную компонента каждого вектора, следуя данным ниже указаниям.

а) Какая из следующих величин представляет собой восточную компоненту вектора В ?

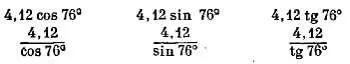
б) Вычислите значение восточной компоненты вектора В , пользуясь таблицами тригонометрических функций (можно взять четырехзначные таблицы, но лучше трехзначные; не тратьте время на вычисления по более точным таблицам). Вычислите также северную компоненту вектора В .

Назовите обе эти компоненты X Ви Y В.

в) Проделайте то же самое для каждого вектора. Вычислите величину и наклон суммы векторов. Обратите внимание, что этот метод не требует вычерчивания в масштабе. Разумеется, им нельзя пользоваться, отрешившись от реальной ситуации и совсем не прибегая к чертежам. В таблицах тригонометрических функций как бы скрыты точные геометрические построения. Подобно числу π , синуса и косинусы, можно вычислить арифметически с помощью бесконечных рядов, но эти ряды, получены на основе геометрических допущений, проверенных сопоставлением с окружающим миром.