Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Фиг. 40. Сложение перемещений.

Если перемещения совершаются одновременно (так бывает, когда полет самолета происходит при наличии ветра) мы можем по-прежнему считать, что сначала происходит одно перемещение, а потом другое, и прийти к результирующему перемещению R (фиг. 41).

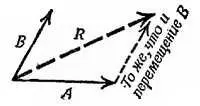
Фиг. 41. Сложение перемещений.

Мы находим результирующее перемещение, беря сначала одно перемещение, а затем другое, как показано на фиг. 42, а или б . Объединяя обе эти фигуры (фиг. 42, в ), мы видим, что результирующее перемещение дается диагональю параллелограмма, сторонами которого служат первоначальные перемещения.

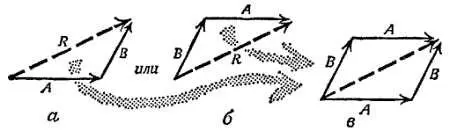
Фиг. 42. Сложение перемещений.

Это правило для сложения перемещений несомненно верно; в этом нас убеждает здравый смысл, основанный на опыте, приобретенном начиная с раннего детства.

Это правило можно обратить и разложить перемещение R на компоненты А и В . Эти компоненты — одна из возможных пар перемещений, которые вместе дают R . Существует бесконечное множество таких пар, каждая из которых дает в сумме одно и точке перемещение R .

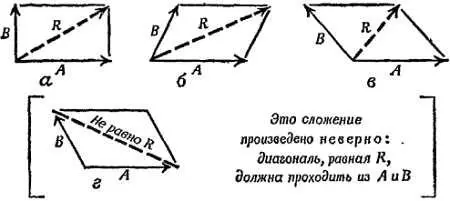
Фиг. 43. Примеры сложения перемещений по правилу параллелограмма.

Задача 6

а) На фиг. 44, а изображено перемещение R , разложенное на две компоненты А 1 и В 1 ; на фиг. 44, б показано то же самое перемещение R , разложенное на другую пару компонент А 2 и В 2 . Скопируйте эти рисунки и добавьте к ним еще несколько, на каждом из которых было бы изображено то же самое перемещение R , разложенное на другие компоненты: А 3, В 3, А 4, В 4 и т. д.

Фиг. 44. Вектор Rможно разложить на компоненты A 1и B 1, A 2и В 2или на другие пары компонент. Компоненты вектора Rне обязательно должны составлять между собой угол 90°.

б) Покажите, что компоненте А можно придать любое направление и любую величину и при этом найти такую компоненту В , которая в сумме с А даст R . (Это равносильно вычитанию векторов R-А , которое находит применение в физике и встретится нам в дальнейшем.)

Скорость

Направление перемещения имеет столь же важное значение, как и величина. В физике скорость связывают с определенным направлением . Скорость обладает обоими качествами: величиной и направлением [30] В обиходном языке, говоря о скорости, имеют в виду, насколько быстро движется предмет по какой-либо траектории — прямолинейной или искривленной. В физике скорость — это перемещение за единицу времени в определенном направлении, представляющее собой вектор. Чтобы задать скорость, указывают число, единицу измерения и направление, например 15 км/час в северном направлении. . Подчиняются ли скорости правилу геометрического сложения? Или, как сказал бы ученый, являются ли скорости «векторами»?

Векторы (определение)

Векторы — это величины, складываемые геометрическим способом . Они называются «векторами» [31] Слово «вектор» происходит от латинского глагола, означающего «везти», «нести» или «транспортировать». потому, что их можно охарактеризовать, проведя отрезок прямой, показывающий как величину вектора (в некотором масштабе), так и его направление.

Правило сложения двух векторов

Геометрическое сложение описывается следующим правилом. (Согласно определению векторов, оно автоматически применимо к ним.)

Чтобы сложить два вектора, выбирают подходящий масштаб и вычерчивают их в этом масштабе из одной точки, а затем строят на складываемых векторах параллелограмм. Тогда сумма векторов будет изображаться диагональю параллелограмма, соединяющей исходную точку с противолежащей вершиной.

При таком способе сложения сумма нескольких векторов определяется как единственный вектор, который может заменить первоначальные векторы, или производит такой же физический эффект.

Подобно тому как векторы А и В дают при сложении сумму R 2(фиг. 45), можно сложить векторы А и В и С , прибавив С к R 2, в результате чего получим вектор R 3. Прибавляя далее вектор D , получаем R 4и т. д. Или, проще говоря, любое количество векторов можно складывать, проводя следующий прибавляемый вектор из конца предыдущего, как показано на фиг. 46 (этот рисунок представляет собой лишь упрощение фиг. 45, б ), и их сумма будет изображаться вектором, соединяющим исходную точку с конечной.

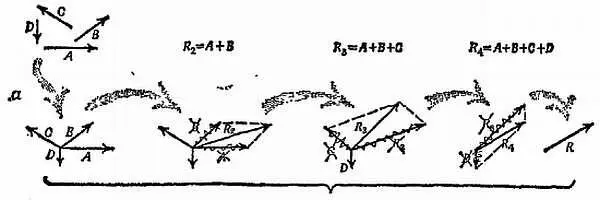
Фиг. 45. Сложение векторов путем построения параллелограмма.

а— этапы построения; б— результат построения.

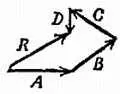
Фиг. 46. Сложение векторов путем построения многоугольника.

Какие величины относятся к векторам? Иначе говоря, какие величины складываются геометрически по правилу параллелограмма? Векторами являются перемещения, или, если называть их более строго, «направленные расстояния» или «смещения». Раз перемещения — векторы, то достаточно разделить их на промежуток времени, за который происходит перемещение, чтобы увидеть, что скорости — тоже векторы. Продолжая этот подход, мы видим, что ускорения — тоже векторы [32] Перемещение — это вектор. Скорость — это ведь перемещение в час, поэтому и скорость — вектор. Следовательно, изменение скорости (приращение или убыль скорости) — тоже вектор. Ускорение есть изменение скорости в час , поэтому и ускорение — вектор. . Нам встретятся и другие векторы, другие величины, которые нужно измерять с помощью приборов и которые подчиняются правилу геометрического сложения?

Здесь возникает важный вопрос: являются ли силы векторами, т. е. подчиняются ли они правилам геометрического сложения?

На этот вопрос нельзя ответить, просто подумав [33] Разве что мы готовы определить силы как величины, складываемые геометрически, а затем принять следствия этого определения при дальнейшем построении механики! . Ответ не очевиден и требует предварительного изучения (см. гл. 3 ).