Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Скаляры

Физические величины, которые имеют только величину и которым нельзя приписать никакого направления, называются скалярами ; хорошими примерами скалярных величин служат объем и температура. Существуют и такие вещи, которые не являются ни векторами, ни скалярами, скажем доброта, а также некоторые величины, этакие «сверхвекторы», называемые тензорами . Примером тензоров могут служить напряжения в деформированном твердом теле: давление, перпендикулярное к любой площадке образца, и срезающие усилия, действующие вдоль нее. Более сложные примеры встречаются в математической теории относительности. Например, мы будем рассматривать количество движения m vкак вектор с тремя компонентами: m v x, m v y, m v z, а кинетическую энергию — как скаляр. Эйнштейн, придерживаясь обобщенного представления о пространстве-времени, предпочитал объединять количество движения и кинетическую энергию в «четырехвектор», т. е. с четырьмя компонентами: три для количества движения и одна для кинетической энергии.

Сложение нескольких векторов

Два вектора складываются по правилу параллелограмма.

Вверху фиг. 47 показано сложение A + B = R (знаки +и =, напечатанные жирным шрифтом, обозначают геометрическое сложение). Исходя из этого определения, мы можем прийти к более примитивным способам сложения «одного перемещения, а потом другого», как показано на фиг. 47.

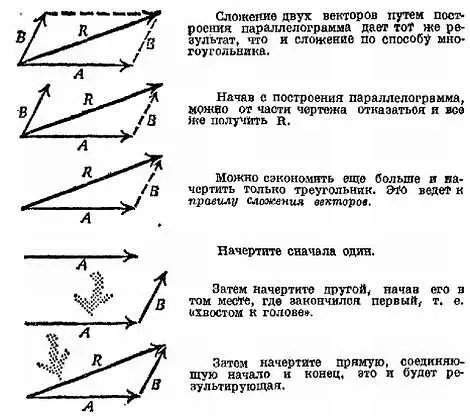
Фиг. 47. Сложение векторов по правилу многоугольника.

Это простейший способ сложения нескольких векторов. Если нам нужно сложить векторы А, В, С, D , то можно было бы складывать их, применяя последовательное построение параллелограмма: получить сумму A + B , прибавить ее к С , а затем прибавить новую сумму к D . Однако такое построение утомительно, и если выполнить все его этапы на одном чертеже, получится изрядная путаница (фиг. 49, а ). Вместо этого сложим А и В по правилам многоугольника, проведя В из конца А , затем прибавим С к их сумме, проведя С из конца этой суммы, затем прибавим D . Можно опустить промежуточные суммы и найти общую сумму R, соединив начало первого вектора с концом последнего (фиг. 49, б).

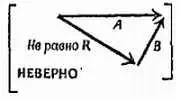
Фиг. 48. Никогда не складывайте векторы «голова к голове».

Получается совершенно неверный ответ, отнюдь не их сумма.

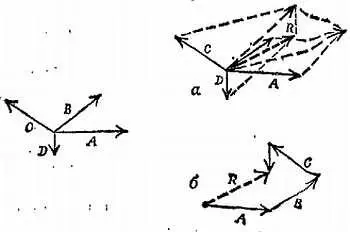
Фиг. 49. Сложение нескольких векторов.

а— методом последовательного построения параллелограммов; б— методом построения многоугольника.

Проведение параллельных прямых

Чтобы переместить вектор с одного места на листе бумаги в другое, нужно начертить на новом месте отрезок прямой, имеющий ту же длину и то же направление, что и прежний отрезок, т. е. новый отрезок должен быть параллелен первому. Существуют геометрические методы и приспособления, позволяющие провести прямую, параллельную другой прямой. Мы покажем вам хотя бы один способ построения параллельных прямых. Для этого не требуется сложного построения углов.

На фиг. 50 показан простой способ проведения параллельных прямых при помощи линейки или обложки книги (или любого прямоугольника или треугольника). Чтобы провести через точку А прямую P ' Q ' параллельную прямой РQ , расположите один край книги вдоль прямой PQ . Приложите к другому краю книги линейку. Прижав линейку к бумаге, перемещайте вдоль нее книгу до тех пор, пока та сторона книги, которую вы совместили с прямой PQ , не пройдет через точку А . Теперь проведите по этой стороне требуемую прямую P'Q' через точку А .

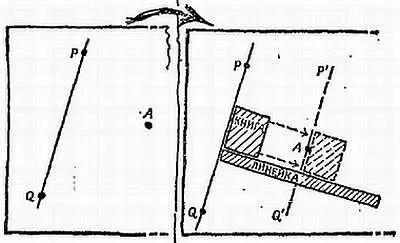
Фиг. 50. Простой способ проведения параллельных прямых.

Задача 7. Сложение скоростей

Корабль, попавший в туман, держит курс на север и идет, как считает штурман, со скоростью 4 м/сек; течение слабое. На самом же деле корабль сносит к востоку течением, скорость которого равна также 4 м/сек. Предположим, что туман, рассеялся и штурман уже может видеть близлежащие острова. В каком направлении, по его наблюдениям, фактически движется корабль? С какой скоростью?

Задача 8. Вычисление векторной суммы

Корабль отправился на, север и движется в тумане со скоростью 4 м/сек, как в задаче 7. Фактически корабль сносит к востоку течением, скорость которого равна 3 м/сек. Чему равна скорость корабля по отношению к суше?

Задача 9. Штурманская задача

Штурман пытается провести судно в тумане через узкий проход между рифами.

а) Он знает, что проход лежит к северо-востоку и что океанское течение сносит судно к востоку со скоростью 5 м/сек. Винт сообщает судну скорость 5 м/сек в направлении вперед. В каком направлении штурман должен вести судно, пользуясь своим компасом? ( Указание . Проведите известный вектор скорости течения. Из начала этого вектора проведите прямую, совпадающую с направлением сумма, а из конца его проведите надлежащим образом вектор скорости, развиваемой судовым двигателем. Достройте параллелограмм.)

б) Представьте себе, что проход между рифами идет в северном направлении, скорость течения равна 5 м/сек, направлено оно на восток, а скорость, сообщаемая судну винтом, равна 9 м/сек. Постройте график и покажите направление, в котором штурман должен, вести судно по компасу.

в) Представьте себе, что проход лежит к северу, а скорость течения равна 5 м/сек, направлено оно на восток. Докажите, что судно можно провести через проход только в том случае, если судовой двигатель позволяет развить скорость больше 5 м/сек.

Влияет ли порядок, в котором складываются векторы, на сумму?

Складывая векторы один за другим по правилу многоугольника, можно было бы располагать их в другом порядке, скажем A, D, С, В …, а не А, В, С, D …, в результате чего получим другой многоугольник. Получим ли мы ту же векторную сумму?

Приводимая ниже задача дает ответ на этот вопрос.

Задача 10

На фиг. 51 показано несколько векторов А, В, С, D, E , которые все проведены, из одной точки О . Сложите эти векторы по правилу многоугольника, т. е. проводя каждый последующий вектор из конца предыдущего, следуя данным ниже указаниям. Приведенный здесь рисунок слишком мал для точного выполнения чертежа и измерений, поэтому прежде всего воспроизведите его в большем масштабе на листе миллиметровки так, чтобы каждой клетке соответствовал квадрат со стороной 2 см. Затем к вектору А , который уже проведен, прибавьте В , затем С , затем D , затем Е , проводя каждый из прибавляемых векторов из конца предыдущего. Для этого вам придется перенести вектора В, С, D, Е при помощи какого-нибудь способа проведения параллельных прямых. (Воспользуйтесь либо данными, взятыми из разграфленной сетки фиг. 51, либо способом, показанным на фиг. 50.)