Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Фиг. 55. К задаче 14.

Задача 15

Воспользовавшись своими знаниями о векторах, покажите, как происходят горизонтальное и вертикальное движения летящего снаряда. На фиг. 56 показана траектория камня, брошенного в воздух. Скопируйте ее приблизительно в более крупном масштабе. Выделите ряд точек на траектории, скажем А, В, С, D, Е , и для каждой точки изобразите на чертеже горизонтальную скорость, вертикальную скорость и действительную (суммарную) скорость движения по примеру, данному для точки D .

Фиг. 56. К задаче 15.

Скорость движения в точке D направлена по касательной к кривой в этой точке.

Анализ построения для точки D. Проведите в точке D касательную DT к траектории. Тогда действительная скорость направлена по касательной DT , Проведите из точки D отрезок горизонтальной прямой Н , который будет характеризовать горизонтальное движение. (Поскольку скорость движения камня неизвестна, считайте, что его горизонтальная скорость изображается отрезком Н , длина которого на фиг. 56 равна 1,1 см.)

Мы рассматриваем действительное движение вдоль DT как составленное из горизонтальной и вертикальной компонент, поэтому мы строим параллелограмм, представляющий собой прямоугольник, у которого Н — одна из сторон, а диагональ направлена по DT . Тогда вертикальная сторона V изображает вертикальную скорость в точке D , а диагональ R — действительную скорость движения по криволинейной траектории. Проделайте подобное построение в каждой из точек А, В, С, D, Е … на вашем рисунке (точные построения делать не нужно) и покажите, какие происходят изменения в движении. При этом не забывайте о важном свойстве горизонтального движения летящего снаряда.

Движение тел и параболы

Форму траектории движения тела можно проанализировать с помощью геометрии или алгебры.

Геометрический анализ . Предположим, что в горизонтальном направлении брошен камень. Камень проходит в своем горизонтальном движении одинаковые расстояния по горизонтали за каждую секунду, совершая в то же время ускоренное движение в вертикальном направлении. Падая, он пролетает по вертикали 4,9 м за первую секунду после начала движения, 19,6 м за первые 2 сек, 43,9 м за первые 3 сек и т. д. Нанесите на масштабную сетку положения камня в различные моменты времени. Выберите промежутки времени от начала движения, которые находятся в пропорции 1:2:3:4…. За эти промежутки времени камень в своем равномерном горизонтальном движении проходит расстояния по горизонтали, которые находятся в той же пропорции 1:2:3:4…

Однако камень, падая, проходит по вертикали расстояния, пропорциональные квадратам этих чисел, т. е. 1, 4, 9, 16…, поскольку

РАССТОЯНИЕ ПО ВЕРТИКАЛИ = 1/ 2∙ g∙(ВРЕМЯ) 2

а значения величины ( время ) 2находятся в пропорции 1:4:9…

Отметьте положение камня в эти равноотстоящие друг от друга моменты времени, проведя вертикальные прямые через равные интервалы, скажем через 2 см; проведите также горизонтальные прямые на расстоянии 1 см вниз до исходного уровня, 4 см, 9 см и т. д., чтобы отметить расстояния по вертикали, пройденные камнем в падении. Тогда предсказанная траектория движения будет отмечена пересечениями вертикальных и горизонтальных прямых, как показано на фиг. 57. Это можно продемонстрировать, бросая шарики или выпуская водяные капли перед доской, на которой проведены такие прямые.

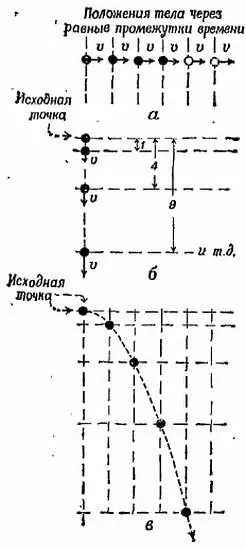
Фиг. 57. Сложение горизонтального и вертикального движений тела.

а— горизонтальное движение (не меняется); б — вертикальное движение с ускорением силы тяжести (свободное падение); в— сложное движение.

Задача 16

Предположим, что опыт убедил нас в том, что движение тел действительно происходит по кривой, проходящей через отмеченные на сетке точки. В какой мере это убеждает нас в правильности представлений о движении в природе? В подобном опыте начальную горизонтальную скорость, сообщаемую телу, нужно выбрать так, чтобы траектория проходила по отметкам (фиг. 58, а ). Предположим, мы уменьшили скорость и отметили на доске новую траекторию движения. Каким образом можно проверить, совершает ли тело такое же движение, что и прежде (фиг. 58, б )?

Фиг. 58. К задаче 16.

Алгебраический- анализ. Начертите на разграфленной бумаге с координатами х и у воображаемую траекторию летящего камня и найдите ее уравнение. Предположим, что камень брошен горизонтально из начала координат (0, 0) со скоростью 5 м/сек. Тогда за каждую секунду камень перемещается в горизонтальном направлении на 5 м. По прошествии t сек после начала движения камень переместится в горизонтальном направлении на 5t м, поэтому можно записать

РАССТОЯНИЕ, ПРОЙДЕННОЕ В ГОРИЗОНТАЛЬНОМ НАПРАВЛЕНИИ, х= 5∙ tм.

Через t сек камень, падая из состояния покоя, пройдет по вертикали расстояние у , определяемое формулой

РАССТОЯНИЕ, ПРОЙДЕННОЕ ПО ВЕРТИКАЛИ, y= 1/ 2УСКОРЕНИЕ t 2= 1/ 2(9,8)∙ t 2 = 4,9∙ t 2 м

Эти формулы справедливы для любой стадии движения камня по его криволинейной траектории, поэтому мы можем записать

x= 5∙ t

y= 4,9∙ t 2

Чтобы найти одно уравнение, описывающее траекторию движения, зададим себе вопрос: «Какое соотношение между х и у обеспечивает выполнение обоих приведенных выше требований на каждом этапе движения камня?» Для любой произвольно выбранной точки на траектории значения ее координат х и у должны удовлетворять обоим приведенным выше уравнениям для соответствующего значения t . Это значение t должно быть одинаковым в обоих уравнениях — ведь это время, когда камень достигает выбранной точки.

Поэтому мы можем избавиться от t , выразив из одного уравнения t и подставив полученное выражение в другое уравнение. Проделаем это.

Уравнение x= 5∙ tдает t= x/5; подставляя выражение х /5 вместо t в уравнение y= 4,9∙ t 2, получаем у= 4,9∙( х/5) 2, или у= (4,9/25)∙ x 2.

Уравнение траекторий движения камня будет тогда иметь вид у= 0,196∙ x 2.

В более общем случае, если камень брошен горизонтально с начальной скоростью v горм/сек и падает с вертикальным ускорением g м/сек на сек, то