Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Бойль сделал замечательное открытие, которое доставило ему большое удовлетворение, — он установил простую связь между давлением воздуха и его объемом. Этим правилом пользуются везде, где имеют дело с газами (в химии, физике и в биологии).

Вы сможете воспроизвести в лаборатории работу Бойля и, вероятно, проверить его открытие более точно, чем он сам. Однако сначала надо уяснить себе смысл понятия давление , поэтому в качестве предварительного опыта следует научиться производить простейшие измерения давления. Выполните измерения и расчеты опыта 5 (а) , прежде чем приступить к проверке закона Бойля — опытам 5 (б) или 5 (в) . Если вы не знакомы с законами давления и с применением U-образных трубок в качестве манометров, прочтите приведенные ниже предварительные замечания. Решите также задачи на давление.

Некоторые сведения о давлении и его измерении

Вода в обоих коленах открытых U-образных трубок устанавливается на одном и том же уровне независимо от формы трубок [51] Если не действуют эффекты поверхностного натяжения, которые становятся заметными в очень тонких трубках. (см. демонстрационные опыты). Это позволяет думать, что равновесие не определяется весом жидкости в каждом колене. В трубке, имеющей колена разного размера, вес жидкости в широком колене значительно больше, чем в узком, и нагрузка на дно обоих колен различна. Но существует некий фактор, который одинаково действует на жидкость по обе стороны от соединительного колена трубки, и оказывается, что это не вес вышележащей жидкости, а сила, действующая на единицу площади , или нагрузка на каждый квадратный сантиметр , которую и называют давлением .

Как говорит пословица, кошке позволено смотреть на короля; ученый имеет полное право силу, приходящуюся на единицу площади, назвать давлением, не имея при этом в виду никакого научного факта. Но мы даем названия только таким величинам, которые особенно полезны. Например, произведение (масса)∙(скорость) полезно, потому что оно сохраняется постоянным, и мы называем его количеством движения . Полезно и отношение (масса)/(объем) , которое дает массу каждой единицы объема [52] При проектировании здании, механизмов, приборов и т. д. объем какой-либо части можно вычислить по чертежам, но часто надо знать ее массу (или ее вес), чтобы определить, сколько надо заказать килограммов или тонн. Массу можно найти, умножив объем на отношение (масса)/(объем) , которое называют плотностью . Это все равно, что найти стоимость нескольких грузовиков путем умножения числа грузовиков на отношение стоимости грузовиков к их числу , которое в этом случае называют ценой грузовика. Таким образом, плотность — это своего рода «цена» материала, выраженная в массе, приходящейся на единицу объема. , поэтому мы называем его плотностью . Мы даем специальное название отношению (сила)/(площадь) (=сила, действующая на каждую единицу площади), потому что оно очень полезно при обращении с жидкостями и газами:

ДАВЛЕНИЕ = СИЛА / ПЛОЩАДЬ

Проработка задач 1–5 научит вас обращению с понятием «давление».

Задача 1

Килограмм∙сила (кГ) — «плохая» единица силы; ньютон — «хорошая» единица.

а) Назовите еще одну «плохую» и еще одну «хорошую» единицу силы.

б) Назовите единицы давления, которые соответствуют каждой из этих четырех единиц силы.

Задача 2

1) Человек весом 68 кГ стоит на прямоугольном бруске из мягкой глины. Верхняя грань бруска имеет размеры 12,5 см х 7,5 см и полностью накрыта подошвой ботинка, которая больше бруска.

а) Какую силу и б) какое давление оказывает человек на глину?

Фиг. 83. К задаче 2.

2) Предположим, что человек сходит с бруска, кладет на глину небольшой деревянный кубик размером 2,5 см х 2,5 см х 2,5 см и становится на верхнюю грань кубика, балансируя на одной ноге.

а) Какую силу и б) какое давление теперь оказывает он на глину?

3) Как различается действие на глину в случаях 1 и 2?

4) Что является более полезной мерой, когда имеешь дело с деформацией глины и т. д., сила или давление

5) Резец для резьбы по дереву имеет клинообразную форму и заканчивается острым лезвием. Укажите причины придания резцу такой формы (их по крайней мере две).

Задача 3

(Эти вопросы, помогают понять принцип действия барометров.)

1) Плотность воды равна 1000 г на 1 дм 3. Что это значит?

2) Удельный вес ртути равен 13,6. Что это значит?

3) Выразите плотность ртути в г/дм 3в виде произведения сомножителей.

4) Выразите плотность ртути в кг/м 3(плотность воды в единицах МКС равна 1000 кг/м 3).

5) Прямоугольный бак имеет основание размером 3 м х 1,5 м; бак заполнен ртутью до глубины 60 см (фиг. 84).

а) Каков вес ртути в баке (в кГ)?

6) Какова сила, действующая на дно бака (в кГ)?

в) Каково давление на дно (в кГ/м 2)?

г) Сколько квадратных сантиметров в 1 м 2?

д) Каково давление на дно (в кГ/см 2)?

6) Предположим, что бак находится внутри второго бака значительно большего размера и больший бак также заполнен ртутью до глубины 60 см, так что слой ртути глубиной 60 см находится как внутри первого бака, так и вне его (см. фиг. 84).

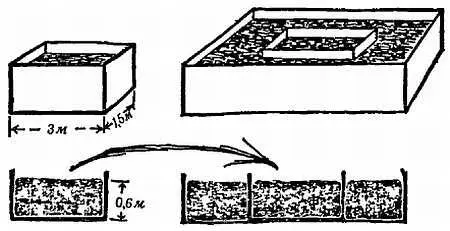
Фиг. 84. Баки со ртутью.

а) Изменятся ли ответы на вопросы 5 для внутреннего бака?

б) Допустим, что первый бак растворился, а ртуть осталась и основание от первого бака также осталось на месте. Останется ли давление на основание тем же (глубина ртути по-прежнему 60 см)?

7) Какие числа нужны для расчета давления ртути на дно бака? Какое число не нужно и почему?

8) Давление можно вычислить с помощью примитивного, простого, но длинного метода деления общего веса жидкости на площадь основания, на котором она находится.

а) При какой площади основания эти вычисления упрощаются?

б) Годится ли этот метод, если боковые стенки наклонны?

Задача 4

Вода удерживается дамбой высотой 12 м и шириной 30 м (фиг. 85). Уровень воды лежит на 3 м ниже верха дамбы. Вода простирается на 2,93 км от дамбы.

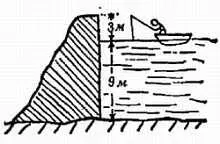
Фиг. 85. К задаче 4.

1) Можно найти общий вес воды, удерживаемой дамбой. Для этого надо использовать величину 2,93 км. Почему для расчета давления на дамбу это значение не нужно? (Другими словами, почему давление воды будет таким же, если вода простирается только на 1,93 км?)